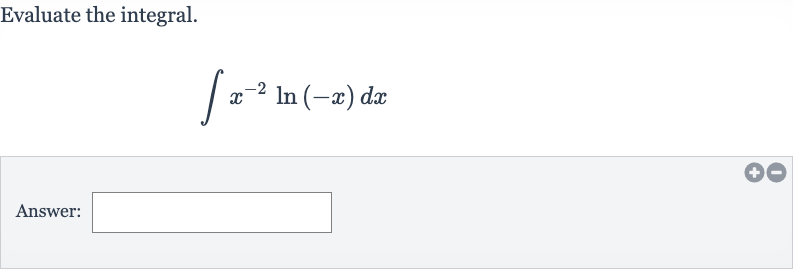
Evaluate the integral. intx^(-2)ln(-x)dx Answer:

Question

Evaluate the integral.  intx^(-2)ln(-x)dx Answer:

Bytelearn · Accepted Answer

Recognize integral involves logarithmic function: Recognize that the integral involves a logarithmic function and a power of x. To solve this, we will use integration by parts, which states that ∫u dv = uv - ∫v du, where u and dv are differentiable functions of x.Choose u and dv: Choose u = ln(-x) and dv = x^(-2)dx. Then we need to find du and v. Differentiating u gives us du = (1/(-x))dx, and integrating dv gives us v = -x^(-1).Apply integration by parts formula: Apply the integration by parts formula: ∫u dv = uv - ∫v du.Substitute u, v, du, dv: Substitute the chosen u, v, du, and dv into the formula to get ∫x^(-2)ln(-x)dx = ln(-x)(-x^(-1)) - ∫(-x^(-1))(1/(-x))dx.Simplify the integral: Simplify the integral: ∫x^(-2)ln(-x)dx = -ln(-x)/x - ∫(1/x^2)dx.Integral of 1/x^2: The integral of 1/x^2 is -1/x. So, we have ∫x^(-2)ln(-x)dx = -ln(-x)/x + 1/x + C, where C is the constant of integration.Combine terms for final answer: Combine the terms to get the final answer: ∫x^(-2)ln(-x)dx = (-ln(-x) - 1)/x + C.

Evaluate the integral. $\newline$ $\int x^{-2} \ln (-x) d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫x−2ln⁡(−x)dx \int x^{-2} \ln (-x) d x ∫x−2ln(−x)dx\newlineAnswer:

Evaluate the integral. $\newline$ $\int x^{-2} \ln (-x) d x$ $\newline$ Answer: