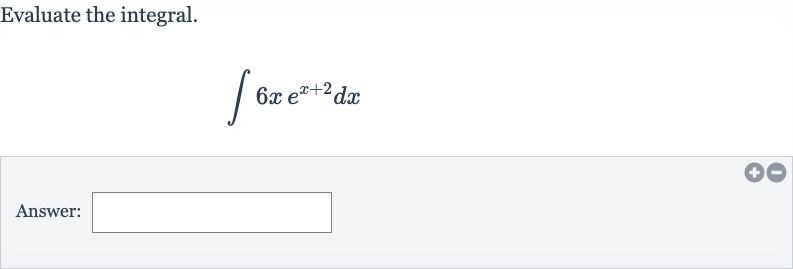Evaluate the integral. int6xe^(x+2)dx Answer:

Question

Evaluate the integral.  int6xe^(x+2)dx Answer:

Bytelearn · Accepted Answer

Choose u and dv: To solve the integral of 6xe^(x+2) with respect to x, we will use integration by parts, which is based on the formula ∫u dv = uv - ∫v du. We need to choose u and dv such that the resulting integral is simpler to solve. Let's choose u = 6x and dv = e^(x+2)dx.Find du and v: We need to find du and v. Differentiating u with respect to x gives us du = 6dx. Integrating dv with respect to x gives us v = e^(x+2).Apply integration by parts: Now we apply the integration by parts formula: ∫u dv = uv - ∫v du ∫6xe^(x+2)dx = 6x * e^(x+2) - ∫e^(x+2) * 6dxIntegrate the second term: We can now integrate the second term: ∫e^(x+2) * 6dx = 6 * ∫e^(x+2)dx To integrate e^(x+2), we use the fact that the integral of e^x is e^x. Therefore, the integral of e^(x+2) is also e^(x+2).Substitute back into formula: So the integral of 6e^(x+2)dx is 6e^(x+2). Now we can substitute this back into our integration by parts formula: ∫6xe^(x+2)dx = 6x * e^(x+2) - 6 * e^(x+2)Simplify the expression: We can simplify the expression: ∫6xe^(x+2)dx = 6xe^(x+2) - 6e^(x+2) + C Here, C is the constant of integration.Final indefinite integral: We have now found the indefinite integral of 6xe^(x+2) with respect to x: ∫6xe^(x+2)dx = 6xe^(x+2) - 6e^(x+2) + C

Evaluate the integral. $\newline$ $\int 6 x e^{x+2} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫6xex+2dx \int 6 x e^{x+2} d x ∫6xex+2dx\newlineAnswer:

Evaluate the integral. $\newline$ $\int 6 x e^{x+2} d x$ $\newline$ Answer: