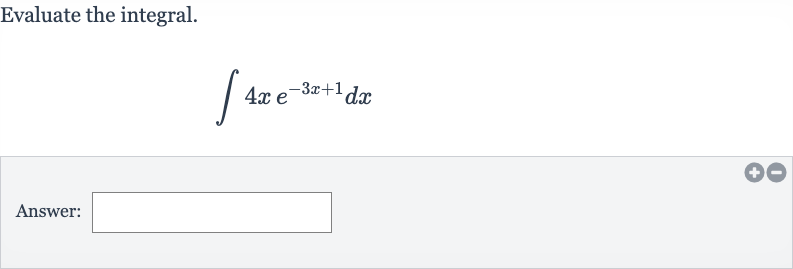
Evaluate the integral. int4xe^(-3x+1)dx Answer:

Question

Evaluate the integral.  int4xe^(-3x+1)dx Answer:

Bytelearn · Accepted Answer

Rewrite Integral: Let's first rewrite the integral to make it clearer: ∫4xe^(-3x+1)dx We can treat the constant term e^1 as a constant multiplier, which can be taken out of the integral. So we rewrite the integral as: 4e * ∫xe^(-3x)dx Now we need to apply integration by parts, where we let u = x (which will be differentiated) and dv = e^(-3x)dx (which will be integrated).Integration by Parts: Differentiate u = x to get du = dx. Integrate dv = e^(-3x)dx to get v. To integrate e^(-3x), we use the fact that the integral of e^(ax) is (1/a)e^(ax), so the integral of e^(-3x) is (-1/3)e^(-3x). Therefore, v = (-1/3)e^(-3x).Substitute u, du, v: Now apply the integration by parts formula: ∫udv = uv - ∫vdu Substitute u, du, v into the formula: ∫xe^(-3x)dx = x*(-1/3)e^(-3x) - ∫(-1/3)e^(-3x)dxIntegrate ∫(-1/3)e^(-3x)dx: Now we need to integrate ∫(-1/3)e^(-3x)dx. As before, the integral of e^(-3x) is (-1/3)e^(-3x), so we get: ∫(-1/3)e^(-3x)dx = (-1/3)*(-1/3)e^(-3x) = (1/9)e^(-3x)Substitute back into formula: Substitute this result back into the integration by parts formula: ∫xe^(-3x)dx = x*(-1/3)e^(-3x) - (1/9)e^(-3x) Now we multiply through by the constant 4e from the original integral: 4e * (x*(-1/3)e^(-3x) - (1/9)e^(-3x))Simplify the expression: Simplify the expression: 4e * (x*(-1/3)e^(-3x) - (1/9)e^(-3x)) = (4e/3)(-x)e^(-3x) - (4e/9)e^(-3x) Now we add the constant of integration C to get the final result: (4e/3)(-x)e^(-3x) - (4e/9)e^(-3x) + C

Evaluate the integral. $\newline$ $\int 4 x e^{-3 x+1} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫4xe−3x+1dx \int 4 x e^{-3 x+1} d x ∫4xe−3x+1dx\newlineAnswer:

Evaluate the integral. $\newline$ $\int 4 x e^{-3 x+1} d x$ $\newline$ Answer: