Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral. int4x^(3)cos(-4x)dx Answer:

Evaluate the integral.\newline∫4x3cos⁡(−4x)dx \int 4 x^{3} \cos (-4 x) d x \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitution and by partsright chevron icon

Full solution

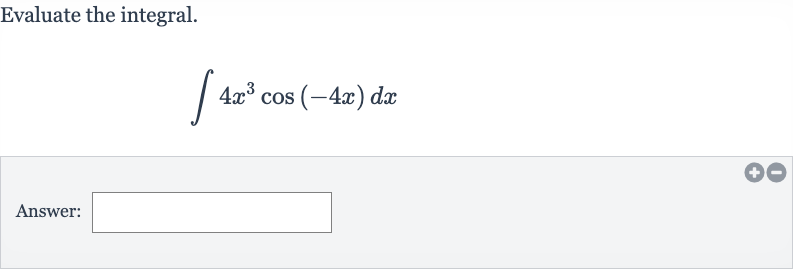
Q. Evaluate the integral.\newline∫4x3cos⁡(−4x)dx \int 4 x^{3} \cos (-4 x) d x \newlineAnswer:
  1. Recognize Integration by Parts: Let's start by recognizing that we can use integration by parts to solve this integral. Integration by parts is given by the formula ∫u dv=uv−∫v du\int u \, dv = uv - \int v \, du, where uu and dvdv are parts of the integrand that we choose. For this integral, we can let u=x3u = x^3 (which will simplify when we differentiate it) and dv=4cos⁡(−4x)dxdv = 4\cos(-4x)dx (which will integrate easily). First, we need to find dudu and vv.\newlineDifferentiate u=x3u = x^3 to get dudu:\newlinedu=d(x3)/dx=3x2dxdu = d(x^3)/dx = 3x^2 dx\newlineIntegrate dv=4cos⁡(−4x)dxdv = 4\cos(-4x)dx to get vv:\newlineuu22\newlineNow we have uu, dudu, vv, and dvdv, so we can apply the integration by parts formula.
  2. Apply Integration by Parts: Apply the integration by parts formula:\newline∫u dv=uv−∫v du\int u \, dv = uv - \int v \, du\newlineSubstitute u=x3u = x^3, du=3x2 dxdu = 3x^2 \, dx, and v=−sin⁡(−4x)v = -\sin(-4x) into the formula:\newline∫4x3cos⁡(−4x) dx=x3(−sin⁡(−4x))−∫(−sin⁡(−4x))(3x2) dx\int 4x^3\cos(-4x)\,dx = x^3(-\sin(-4x)) - \int(-\sin(-4x))(3x^2)\,dx\newlineSimplify the expression:\newline∫4x3cos⁡(−4x) dx=−x3sin⁡(−4x)+∫3x2sin⁡(−4x) dx\int 4x^3\cos(-4x)\,dx = -x^3\sin(-4x) + \int 3x^2\sin(-4x)\,dx\newlineNow we need to integrate ∫3x2sin⁡(−4x) dx\int 3x^2\sin(-4x)\,dx, which again requires integration by parts.
  3. Apply Integration by Parts Again: For the new integral ∫3x2sin⁡(−4x) dx\int 3x^2\sin(-4x)\,dx, we will use integration by parts again. Let's choose u=x2u = x^2 and dv=3sin⁡(−4x) dxdv = 3\sin(-4x)\,dx this time.\newlineDifferentiate u=x2u = x^2 to get dudu:\newlinedu=d(x2)/dx=2x dxdu = d(x^2)/dx = 2x \,dx\newlineIntegrate dv=3sin⁡(−4x) dxdv = 3\sin(-4x)\,dx to get vv:\newlinev=∫3sin⁡(−4x) dx=(1/(−4))(−cos⁡(−4x))⋅3=−3/4cos⁡(−4x)v = \int 3\sin(-4x)\,dx = (1/(-4))(-\cos(-4x)) \cdot 3 = -3/4\cos(-4x)\newlineNow we have new uu, dudu, vv, and u=x2u = x^222, so we can apply the integration by parts formula again.
  4. Integrate by Substitution: Apply the integration by parts formula to the new integral: \newline∫u dv=uv−∫v du\int u \, dv = uv - \int v \, du\newlineSubstitute u=x2u = x^2, du=2x dxdu = 2x \, dx, and v=−34cos⁡(−4x)v = -\frac{3}{4}\cos(-4x) into the formula:\newline∫3x2sin⁡(−4x) dx=x2(−34cos⁡(−4x))−∫(−34cos⁡(−4x))(2x) dx\int 3x^2\sin(-4x)\,dx = x^2(-\frac{3}{4}\cos(-4x)) - \int(-\frac{3}{4}\cos(-4x))(2x)\,dx\newlineSimplify the expression:\newline∫3x2sin⁡(−4x) dx=−34x2cos⁡(−4x)+32∫xcos⁡(−4x) dx\int 3x^2\sin(-4x)\,dx = -\frac{3}{4}x^2\cos(-4x) + \frac{3}{2}\int x\cos(-4x)\,dx\newlineNow we need to integrate ∫xcos⁡(−4x) dx\int x\cos(-4x)\,dx, which is a simpler integral that can be solved directly.
  5. Apply Integration by Parts Once More: To integrate ∫xcos⁡(−4x) dx\int x\cos(-4x)\,dx, we can use a simple substitution. Let w=−4xw = -4x, then dw=−4 dxdw = -4\,dx, or dx=−dw4dx = -\frac{dw}{4}. Substitute ww and dwdw into the integral: ∫xcos⁡(−4x) dx=∫(−14)wcos⁡(w)(−dw4)\int x\cos(-4x)\,dx = \int(-\frac{1}{4})w\cos(w)(-\frac{dw}{4}) Simplify the expression: ∫xcos⁡(−4x) dx=(116)∫wcos⁡(w) dw\int x\cos(-4x)\,dx = (\frac{1}{16})\int w\cos(w)\,dw Now we can integrate ∫wcos⁡(w) dw\int w\cos(w)\,dw using integration by parts one more time.
  6. Substitute Back for Final Answer: For the integral ∫wcos⁡(w) dw\int w\cos(w)\,dw, let's use integration by parts one last time. Choose u=wu = w and dv=cos⁡(w) dwdv = \cos(w)\,dw.\newlineDifferentiate u=wu = w to get dudu:\newlinedu=dwdu = dw\newlineIntegrate dv=cos⁡(w) dwdv = \cos(w)\,dw to get vv:\newlinev=∫cos⁡(w) dw=sin⁡(w)v = \int\cos(w)\,dw = \sin(w)\newlineNow apply the integration by parts formula:\newline∫u dv=uv−∫v du\int u\, dv = uv - \int v\, du\newlineSubstitute u=wu = w, du=dwdu = dw, and u=wu = w22 into the formula:\newlineu=wu = w33\newlineIntegrate u=wu = w44:\newlineu=wu = w55\newlineNow substitute back into the integration by parts expression:\newlineu=wu = w66\newlineNow we need to substitute back for u=wu = w77 to get the integral in terms of u=wu = w88.
  7. Substitute Back for Final Answer: For the integral ∫wcos⁡(w) dw\int w\cos(w)\,dw, let's use integration by parts one last time. Choose u=wu = w and dv=cos⁡(w) dwdv = \cos(w)\,dw.\newlineDifferentiate u=wu = w to get dudu:\newlinedu=dwdu = dw\newlineIntegrate dv=cos⁡(w) dwdv = \cos(w)\,dw to get vv:\newlinev=∫cos⁡(w) dw=sin⁡(w)v = \int\cos(w)\,dw = \sin(w)\newlineNow apply the integration by parts formula:\newline∫u dv=uv−∫v du\int u\, dv = uv - \int v\, du\newlineSubstitute u=wu = w, du=dwdu = dw, and u=wu = w22 into the formula:\newlineu=wu = w33\newlineIntegrate u=wu = w44:\newlineu=wu = w55\newlineNow substitute back into the integration by parts expression:\newlineu=wu = w66\newlineNow we need to substitute back for u=wu = w77 to get the integral in terms of u=wu = w88.Substitute u=wu = w77 back into the integral result:\newlineu=wu = w66\newlinedv=cos⁡(w) dwdv = \cos(w)\,dw11\newlineNow we have all the parts needed to write down the final answer for the original integral.
  8. Substitute Back for Final Answer: For the integral ∫wcos⁡(w) dw\int w\cos(w)\,dw, let's use integration by parts one last time. Choose u=wu = w and dv=cos⁡(w) dwdv = \cos(w)\,dw.

    Differentiate u=wu = w to get dudu:
    du=dwdu = dw

    Integrate dv=cos⁡(w) dwdv = \cos(w)\,dw to get vv:
    v=∫cos⁡(w) dw=sin⁡(w)v = \int\cos(w)\,dw = \sin(w)

    Now apply the integration by parts formula:
    ∫u dv=uv−∫v du\int u\, dv = uv - \int v\, du

    Substitute u=wu = w, du=dwdu = dw, and u=wu = w22 into the formula:
    u=wu = w33

    Integrate u=wu = w44:
    u=wu = w55

    Now substitute back into the integration by parts expression:
    u=wu = w66

    Now we need to substitute back for u=wu = w77 to get the integral in terms of u=wu = w88.Substitute u=wu = w77 back into the integral result:
    u=wu = w66
    dv=cos⁡(w) dwdv = \cos(w)\,dw11

    Now we have all the parts needed to write down the final answer for the original integral.Combine all the parts from the integration by parts steps to write the final answer for the original integral:

    dv=cos⁡(w) dwdv = \cos(w)\,dw22

    Simplify the expression:
    dv=cos⁡(w) dwdv = \cos(w)\,dw33

    This is the final answer for the indefinite integral.

More problems from Find indefinite integrals using the substitution and by parts

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

View all (114)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant