AI tutor
Full solution
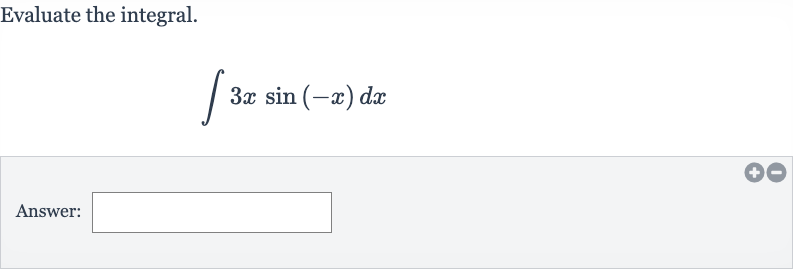
Q. Evaluate the integral.Answer:
- Write Integral: Write down the integral to be evaluated.
- Factor Out Constant: Use the property of integrals that , where is a constant, to factor out the constant .
- Apply Trig Identity: Apply the trigonometric identity to simplify the integrand.
- Integration by Parts: Use integration by parts, where and . Then we need to find and .Let , so .Let , so .
- Find and : Apply the integration by parts formula .
- Apply Integration by Parts: Integrate with respect to .
- Integrate : Substitute the integral of back into the equation., where is the constant of integration.
- Substitute Integral: Simplify the expression.