Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral. int3x cos(-2x+2)dx Answer:

Evaluate the integral.\newline∫3xcos⁡(−2x+2)dx \int 3 x \cos (-2 x+2) d x \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitution and by partsright chevron icon

Full solution

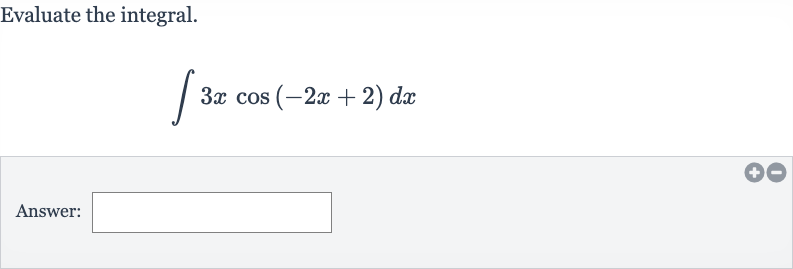
Q. Evaluate the integral.\newline∫3xcos⁡(−2x+2)dx \int 3 x \cos (-2 x+2) d x \newlineAnswer:
  1. Identify Integral: Let's first identify the integral we need to evaluate:\newlineI=∫3xcos⁡(−2x+2) dxI = \int 3x \cos(-2x+2)\,dx\newlineThis is an integration problem that involves a trigonometric function and a polynomial. We can use integration by parts, which is based on the formula ∫u dv=uv−∫v du\int u\, dv = uv - \int v\, du, where uu and dvdv are parts of the integrand that we choose.
  2. Choose uu and dvdv: Choose uu and dvdv for integration by parts. A good choice here is to let u=3xu = 3x (since its derivative is simpler) and dv=cos⁡(−2x+2) dxdv = \cos(-2x+2)\,dx (since the integral of the cosine function is straightforward).\newlineSo, we have:\newlineu=3xu = 3x\newlinedu=3 dxdu = 3\,dx\newlinedv=cos⁡(−2x+2) dxdv = \cos(-2x+2)\,dx\newlinev=∫cos⁡(−2x+2) dxv = \int \cos(-2x+2)\,dx
  3. Find vv: Now we need to find vv by integrating dvdv. To integrate cos⁡(−2x+2)\cos(-2x+2), we can use a substitution. Let w=−2x+2w = -2x+2, then dw=−2dxdw = -2dx. We need to adjust for the −2-2, so we multiply by −12-\frac{1}{2} outside the integral to compensate for the change of variables.\newlinev=∫cos⁡(−2x+2)dxv = \int \cos(-2x+2)dx\newlinev=∫cos⁡(w)(−12)dwv = \int \cos(w)(-\frac{1}{2})dw (after substitution and adjustment)\newlinevv00\newlinevv11\newlineNow we substitute back for vv22 to get vv in terms of vv44.\newlinevv55
  4. Apply Integration by Parts: Now that we have uu, dudu, and vv, we can apply the integration by parts formula:\newlineI=uv−∫vduI = uv - \int v du\newlineI=(3x)(−12)sin⁡(−2x+2)−∫(−12)sin⁡(−2x+2)(3dx)I = (3x)(-\frac{1}{2})\sin(-2x+2) - \int(-\frac{1}{2})\sin(-2x+2)(3dx)\newlineI=(−32)xsin⁡(−2x+2)−∫(−32)sin⁡(−2x+2)dxI = (-\frac{3}{2})x\sin(-2x+2) - \int(-\frac{3}{2})\sin(-2x+2)dx
  5. Integrate Second Term: Next, we need to integrate the second term. We can use the substitution method again with w=−2x+2w = -2x+2, dw=−2dxdw = -2dx, and adjust for the −2-2 as before.\newline∫(−32)sin⁡(−2x+2)dx=(−32)∫sin⁡(w)(−12)dw\int(-\frac{3}{2})\sin(-2x+2)dx = (-\frac{3}{2})\int\sin(w)(-\frac{1}{2})dw\newline=(34)∫sin⁡(w)dw= (\frac{3}{4})\int\sin(w)dw\newline=(34)(−cos⁡(w))= (\frac{3}{4})(-\cos(w))\newlineSubstitute back for ww to get the integral in terms of xx.\newline=(34)(−cos⁡(−2x+2))= (\frac{3}{4})(-\cos(-2x+2))\newline=−(34)cos⁡(−2x+2)= -(\frac{3}{4})\cos(-2x+2)
  6. Combine Results: Combine the results from the integration by parts formula:\newlineI=(−32)xsin⁡(−2x+2)−(−34)cos⁡(−2x+2)+CI = \left(-\frac{3}{2}\right)x\sin\left(-2x+2\right) - \left(-\frac{3}{4}\right)\cos\left(-2x+2\right) + C\newlineSimplify the expression:\newlineI=(−32)xsin⁡(−2x+2)+34cos⁡(−2x+2)+CI = \left(-\frac{3}{2}\right)x\sin\left(-2x+2\right) + \frac{3}{4}\cos\left(-2x+2\right) + C

More problems from Find indefinite integrals using the substitution and by parts

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

View all (114)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant