AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Evaluate the integral.Answer:
Full solution
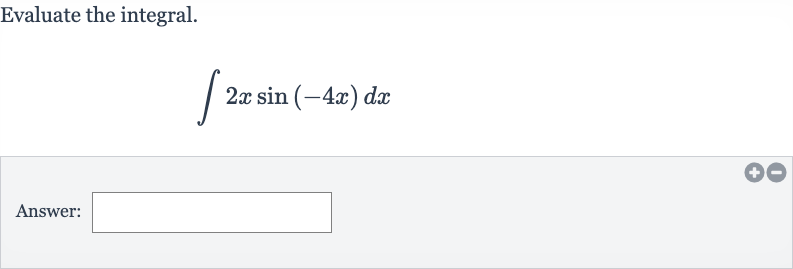
Q. Evaluate the integral.Answer:
- Set Up Integral: Let's start by setting up the integral that we need to evaluate:This is a product of two functions, so we will use integration by parts, which states that .We need to choose and such that the resulting integral is simpler to solve. Let's choose and .
- Choose and : Now we need to find and .To find , we differentiate with respect to :To find , we integrate with respect to :To integrate , we use the substitution method. Let , then , or .Now we substitute back : (since cosine is an even function)
- Find and : Now we apply the integration by parts formula:I = (\frac{\(1\)}{\(2\)})x \cos(\(4\)x) - (\frac{\(1\)}{\(2\)})\int\cos(\(4\)x) dx
- Apply Integration by Parts: Next, we need to integrate \(\cos(4x)\) with respect to \(x\). Let's use the substitution method again. Let \(z = 4x\), then \(dz = 4 dx\), or \(dx = dz/4\). \(\int \cos(4x) dx = \int \cos(z) \cdot (dz/4) = \frac{1}{4} \int \cos(z) dz = \frac{1}{4} \sin(z)\) Now we substitute back \(z = 4x\): \(\int \cos(4x) dx = \frac{1}{4} \sin(4x)\)
- Integrate \(\cos(4x)\): Now we can substitute this result back into our integral: \(I = \frac{1}{2}x \cos(4x) - \frac{1}{2}\left(\frac{1}{4} \sin(4x)\right)\) \(I = \frac{1}{2}x \cos(4x) - \frac{1}{8}\sin(4x)\)
- Substitute Result: Finally, we add the constant of integration \(C\) to our result:\(\newline\)I = \left(\frac{}{}\right)x \cos(x) - \left(\frac{}{}\right)\sin(x) + C
