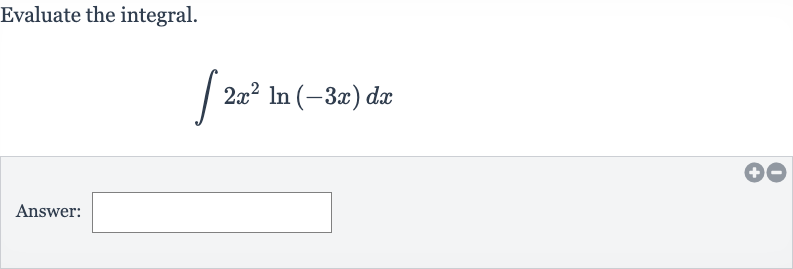
Evaluate the integral. int2x^(2)ln(-3x)dx Answer:

Question

Evaluate the integral.  int2x^(2)ln(-3x)dx Answer:

Bytelearn · Accepted Answer

Define u and dv: Let's use integration by parts to solve the integral $ \int 2x^2 \ln(-3x) \, dx $. We can let $ u = \ln(-3x) $ and $ dv = 2x^2 \, dx $. Then we need to find $ du $ and $ v $.Find du: To find $ du $, we differentiate $ u $ with respect to $ x $: $ du = \frac{d}{dx} \ln(-3x) \, dx = \frac{1}{-3x} \cdot -3 \, dx = \frac{-3}{-3x} \, dx = \frac{1}{x} \, dx $.Find v: To find $ v $, we integrate $ dv $: $ v = \int 2x^2 \, dx = \frac{2}{3}x^3 $.Apply integration by parts formula: Now we apply the integration by parts formula $ \int u \, dv = uv - \int v \, du $: $ \int 2x^2 \ln(-3x) \, dx = uv - \int v \, du $.Substitute into formula: Substitute $ u $, $ v $, $ du $, and $ dv $ into the integration by parts formula: $ \int 2x^2 \ln(-3x) \, dx = \ln(-3x) \cdot \frac{2}{3}x^3 - \int \frac{2}{3}x^3 \cdot \frac{1}{x} \, dx $.Simplify the integral: Simplify the integral: $ \int 2x^2 \ln(-3x) \, dx = \frac{2}{3}x^3 \ln(-3x) - \int \frac{2}{3}x^2 \, dx $.Integrate v: Integrate $ \frac{2}{3}x^2 $ with respect to $ x $: $ \int \frac{2}{3}x^2 \, dx = \frac{2}{3} \cdot \frac{x^3}{3} = \frac{2}{9}x^3 $.Combine terms for final answer: Combine the terms to get the final answer: $ \int 2x^2 \ln(-3x) \, dx = \frac{2}{3}x^3 \ln(-3x) - \frac{2}{9}x^3 + C $, where $ C $ is the constant of integration.

Evaluate the integral. $\newline$ $\int 2 x^{2} \ln (-3 x) d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫2x2ln⁡(−3x)dx \int 2 x^{2} \ln (-3 x) d x ∫2x2ln(−3x)dx\newlineAnswer:

Evaluate the integral. $\newline$ $\int 2 x^{2} \ln (-3 x) d x$ $\newline$ Answer: