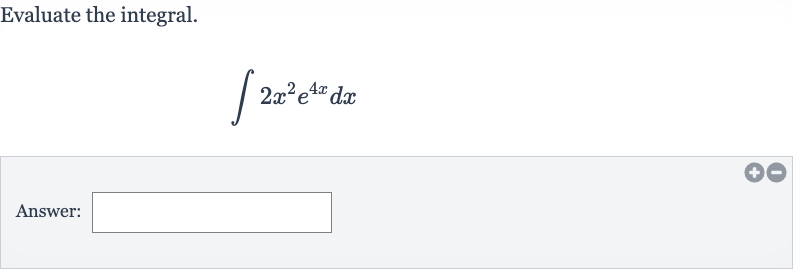
Evaluate the integral. int2x^(2)e^(4x)dx Answer:

Question

Evaluate the integral.  int2x^(2)e^(4x)dx Answer:

Bytelearn · Accepted Answer

Identify Integral: Let's start by identifying the integral we need to evaluate: I = ∫2x^2e^(4x)dx This integral suggests the use of integration by parts, where we let one part be differentiated and the other be integrated. We can choose u = x^2 and dv = 2e^(4x)dx.Choose u and dv: Now we need to find du and v. Differentiating u gives us du = 2xdx, and integrating dv gives us v = (1/2)e^(4x) (since the integral of e^(ax) is (1/a)e^(ax)).Find du and v: Applying the integration by parts formula, ∫udv = uv - ∫vdu, we get: I = uv - ∫vdu I = x^2 * (1/2)e^(4x) - ∫(1/2)e^(4x) * 2xdxApply Integration by Parts: Simplify the integral: I = (1/2)x^2e^(4x) - ∫xe^(4x)dx Now we need to apply integration by parts again to the remaining integral, ∫xe^(4x)dx. This time, let's choose u = x and dv = e^(4x)dx.Simplify Integral: Differentiating u gives us du = dx, and integrating dv gives us v = (1/4)e^(4x).Apply Integration by Parts Again: Applying the integration by parts formula again, we get: I = (1/2)x^2e^(4x) - (x * (1/4)e^(4x) - ∫(1/4)e^(4x)dx)Simplify Integral: Simplify the integral and calculate the last integral: I = (1/2)x^2e^(4x) - (1/4)xe^(4x) + (1/4) * (1/4)e^(4x) I = (1/2)x^2e^(4x) - (1/4)xe^(4x) + (1/16)e^(4x)Calculate Last Integral: Finally, we add the constant of integration C to our result: I = (1/2)x^2e^(4x) - (1/4)xe^(4x) + (1/16)e^(4x) + C

Evaluate the integral. $\newline$ $\int 2 x^{2} e^{4 x} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫2x2e4xdx \int 2 x^{2} e^{4 x} d x ∫2x2e4xdx\newlineAnswer:

Evaluate the integral. $\newline$ $\int 2 x^{2} e^{4 x} d x$ $\newline$ Answer: