Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral. int2x^(2)4^(-2x)dx Answer:

Evaluate the integral.\newline∫2x24−2xdx \int 2 x^{2} 4^{-2 x} d x \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitution and by partsright chevron icon

Full solution

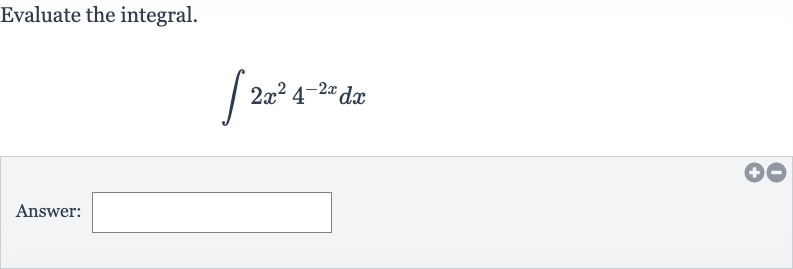
Q. Evaluate the integral.\newline∫2x24−2xdx \int 2 x^{2} 4^{-2 x} d x \newlineAnswer:
  1. Denote Integral: Let's denote the integral by II:I=∫2x2⋅4−2x dxI = \int 2x^2 \cdot 4^{-2x} \, dxTo solve this integral, we will use integration by parts, which states that ∫u dv=uv−∫v du\int u \, dv = uv - \int v \, du, where uu and dvdv are differentiable functions of xx. We need to choose uu and dvdv such that the resulting integral is simpler to solve. Let's choose:u=x2u = x^2 (which implies du=2x dxdu = 2x \, dx)dv=2⋅4−2x dxdv = 2 \cdot 4^{-2x} \, dx (which implies v=∫2⋅4−2x dxv = \int 2 \cdot 4^{-2x} \, dx) Now we need to find vv by integrating dvdv.
  2. Integration by Parts: To find vv, we integrate dvdv:
    v=∫2⋅4−2x dxv = \int 2 \cdot 4^{-2x} \, dx
    We can rewrite 4−2x4^{-2x} as (22)−2x=2−4x(2^2)^{-2x} = 2^{-4x}.
    Now, v=∫2⋅2−4x dxv = \int 2 \cdot 2^{-4x} \, dx
    To integrate this, we use the fact that ∫akx dx=(1k⋅ln⁡(a))⋅akx\int a^{kx} \, dx = (\frac{1}{k} \cdot \ln(a)) \cdot a^{kx}, where a > 0, a≠1a \neq 1, and kk is a constant.
    dvdv00
    dvdv11
    Now we have vv, we can proceed to apply the integration by parts formula.
  3. Find vv: Applying integration by parts:\newlineI=uv−∫vduI = uv - \int v du\newlineI=x2∗(−1/(2ln⁡(2))∗2−4x)−∫(−1/(2ln⁡(2))∗2−4x)∗2xdxI = x^2 * (-1/(2\ln(2)) * 2^{-4x}) - \int(-1/(2\ln(2)) * 2^{-4x}) * 2x dx\newlineSimplify the expression:\newlineI=−x22ln⁡(2)∗2−4x+1ln⁡(2)∫x∗2−4xdxI = -\frac{x^2}{2\ln(2)} * 2^{-4x} + \frac{1}{\ln(2)} \int x * 2^{-4x} dx\newlineNow we need to integrate the remaining integral, which again requires integration by parts.
  4. Apply Integration by Parts: We need to integrate ∫x⋅2−4x dx\int x \cdot 2^{-4x} \, dx by parts again. Let's choose new uu and dvdv:
    u=xu = x (which implies du=dxdu = dx)
    dv=2−4x dxdv = 2^{-4x} \, dx (which implies v=∫2−4x dxv = \int 2^{-4x} \, dx)
    We already found the integral of 2−4x dx2^{-4x} \, dx in a previous step, so:
    v=−14ln⁡(2)⋅2−4xv = -\frac{1}{4\ln(2)} \cdot 2^{-4x}
    Now we apply integration by parts again.
  5. Integrate Again: Applying integration by parts to the new integral:\newline∫x⋅2−4x dx=uv−∫v du\int x \cdot 2^{-4x} \, dx = uv - \int v \, du\newline= x⋅(−12ln⁡(2)⋅2−4x)−∫(−12ln⁡(2)⋅2−4x) dxx \cdot \left(-\frac{1}{2\ln(2)} \cdot 2^{-4x}\right) - \int\left(-\frac{1}{2\ln(2)} \cdot 2^{-4x}\right) \, dx\newlineSimplify the expression:\newline= −x2ln⁡(2)⋅2−4x+12ln⁡(2)∫2−4x dx-\frac{x}{2\ln(2)} \cdot 2^{-4x} + \frac{1}{2\ln(2)} \int 2^{-4x} \, dx\newlineWe already know the integral of 2−4x dx2^{-4x} \, dx, so we can write it down directly:\newline= −x2ln⁡(2)⋅2−4x+12ln⁡(2)⋅(−14ln⁡(2))⋅2−4x-\frac{x}{2\ln(2)} \cdot 2^{-4x} + \frac{1}{2\ln(2)} \cdot \left(-\frac{1}{4\ln(2)}\right) \cdot 2^{-4x}\newline= −x2ln⁡(2)⋅2−4x−18(ln⁡(2))2⋅2−4x-\frac{x}{2\ln(2)} \cdot 2^{-4x} - \frac{1}{8(\ln(2))^2} \cdot 2^{-4x}\newlineNow we can substitute this result back into our original integration by parts formula.
  6. Apply Integration Again: Substituting the result back into the original integration by parts formula:\newlineI=−x22ln⁡(2)⋅2−4x+1ln⁡(2)⋅(−x2ln⁡(2)⋅2−4x−18(ln⁡(2))2⋅2−4x)I = -\frac{x^2}{2\ln(2)} \cdot 2^{-4x} + \frac{1}{\ln(2)} \cdot \left(-\frac{x}{2\ln(2)} \cdot 2^{-4x} - \frac{1}{8(\ln(2))^2} \cdot 2^{-4x}\right)\newlineCombine like terms:\newlineI=−x22ln⁡(2)⋅2−4x−x2(ln⁡(2))2⋅2−4x−18(ln⁡(2))3⋅2−4x+CI = -\frac{x^2}{2\ln(2)} \cdot 2^{-4x} - \frac{x}{2(\ln(2))^2} \cdot 2^{-4x} - \frac{1}{8(\ln(2))^3} \cdot 2^{-4x} + C\newlineThis is the final result of the integral, where CC is the constant of integration.

More problems from Find indefinite integrals using the substitution and by parts

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

View all (114)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant