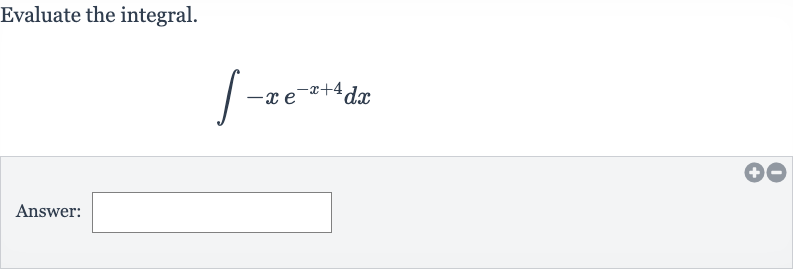
Evaluate the integral. int-xe^(-x+4)dx Answer:

Question

Evaluate the integral.  int-xe^(-x+4)dx Answer:

Bytelearn · Accepted Answer

Recognize problem type: Recognize the integral as an integration by parts problem. Integration by parts formula is ∫u dv = uv - ∫v du. Let u = -x and dv = e^(-x+4)dx.Define u and dv: Differentiate u and integrate dv. du = -dx and v = ∫e^(-x+4)dx. To integrate dv, we need to find the antiderivative of e^(-x+4).Differentiate and integrate: Calculate the antiderivative of e^(-x+4). v = ∫e^(-x+4)dx = e^(-x+4) * (-1) = -e^(-x+4).Calculate antiderivative: Apply the integration by parts formula. ∫u dv = uv - ∫v du. Substitute u, du, and v into the formula.Apply integration by parts: Perform the substitution and simplify. ∫-xe^(-x+4)dx = -x(-e^(-x+4)) - ∫(-e^(-x+4))(-dx). Simplify the expression.Perform substitution: Simplify the expression further. ∫-xe^(-x+4)dx = xe^(-x+4) - ∫e^(-x+4)dx. Now we need to integrate e^(-x+4) with respect to x.Simplify expression: Integrate e^(-x+4) with respect to x. ∫e^(-x+4)dx = e^(-x+4) * (-1) = -e^(-x+4).Integrate e^(-x+4): Substitute the integral back into the expression. xe^(-x+4) - ∫e^(-x+4)dx = xe^(-x+4) - (-e^(-x+4)).Substitute integral back: Simplify the final expression and add the constant of integration. xe^(-x+4) + e^(-x+4) + C.Simplify final expression: Write the final answer. The integral of -xe^(-x+4) with respect to x is xe^(-x+4) + e^(-x+4) + C.

Evaluate the integral. $\newline$ $\int-x e^{-x+4} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫−xe−x+4dx \int-x e^{-x+4} d x ∫−xe−x+4dx\newlineAnswer:

Evaluate the integral. $\newline$ $\int-x e^{-x+4} d x$ $\newline$ Answer: