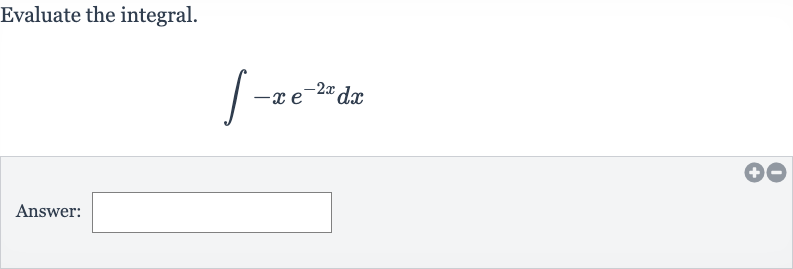
Evaluate the integral. int-xe^(-2x)dx Answer:

Question

Evaluate the integral.  int-xe^(-2x)dx Answer:

Bytelearn · Accepted Answer

Use Integration by Parts: Let's use integration by parts to solve the integral of -xe^(-2x) with respect to x. Integration by parts is given by the formula ∫u dv = uv - ∫v du, where u and dv are parts of the integrand that we choose. We will let u = -x and dv = e^(-2x)dx. Then we need to find du and v.Find du: First, we differentiate u to find du. Since u = -x, we have du = -dx.Find v: Next, we integrate dv to find v. Since dv = e^(-2x)dx, we have v = ∫e^(-2x)dx. To integrate e^(-2x), we use the fact that ∫e^(ax)dx = (1/a)e^(ax) + C, where a is a constant. Therefore, v = (-1/2)e^(-2x).Apply Integration by Parts Formula: Now we apply the integration by parts formula: ∫u dv = uv - ∫v du. Substituting the values we found, we get ∫-xe^(-2x)dx = uv - ∫v du = (-x)(-1/2)e^(-2x) - ∫(-1/2)e^(-2x)(-dx).Simplify the Integral: Simplify the integral: ∫-xe^(-2x)dx = (1/2)xe^(-2x) - ∫(1/2)e^(-2x)dx.Integrate (1/2)e^(-2x): Now we need to integrate (1/2)e^(-2x) with respect to x. As before, we use the fact that ∫e^(ax)dx = (1/a)e^(ax) + C. So, ∫(1/2)e^(-2x)dx = (1/2)(-1/2)e^(-2x) = (-1/4)e^(-2x) + C.Combine Terms: Combine the terms to get the final answer: ∫-xe^(-2x)dx = (1/2)xe^(-2x) - ((-1/4)e^(-2x) + C).Final Answer: Simplify the expression to get the final answer: ∫-xe^(-2x)dx = (1/2)xe^(-2x) + (1/4)e^(-2x) + C.

Evaluate the integral. $\newline$ $\int-x e^{-2 x} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫−xe−2xdx \int-x e^{-2 x} d x ∫−xe−2xdx\newlineAnswer:

Evaluate the integral. $\newline$ $\int-x e^{-2 x} d x$ $\newline$ Answer: