AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Evaluate the integral.Answer:
Full solution
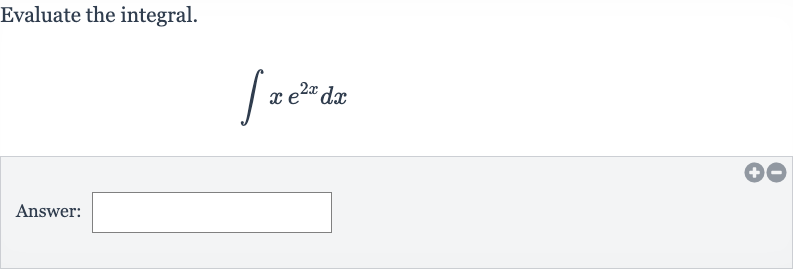
Q. Evaluate the integral.Answer:
- Choose and : To solve the integral of with respect to , we will use integration by parts, which is given by the formula , where and are parts of the integrand that we choose.
- Apply integration by parts: Let's choose (which will be differentiated) and (which will be integrated). Differentiating gives us , and integrating gives us .
- Integrate dv: Now we apply the integration by parts formula: . Substituting the chosen parts, we get $\int x e^{\(2\)x} dx = x \left(\frac{\(1\)}{\(2\)}\right)e^{\(2\)x} - \int \left(\frac{\(1\)}{\(2\)}\right)e^{\(2\)x} dx.
- Substitute back: Next, we integrate \((1/2)e^{2x}\) with respect to \(x\), which gives us \((1/2)\cdot(1/2)e^{2x} = (1/4)e^{2x}\).
- Final result: Substituting this back into our equation, we have \(\int x e^{2x} dx = \left(\frac{1}{2}\right) x e^{2x} - \left(\frac{1}{4}\right) e^{2x} + C\), where \(C\) is the constant of integration.
- Final result: Substituting this back into our equation, we have \(\int xe^{2x}\,dx = \frac{1}{2}xe^{2x} - \frac{1}{4}e^{2x} + C\), where \(C\) is the constant of integration.Therefore, the integral of \(xe^{2x}\) with respect to \(x\) is \(\frac{1}{2}xe^{2x} - \frac{1}{4}e^{2x} + C\).
