Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral. int-x cos(-2x+6)dx Answer:

Evaluate the integral.\newline∫−xcos⁡(−2x+6)dx \int-x \cos (-2 x+6) d x \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitution and by partsright chevron icon

Full solution

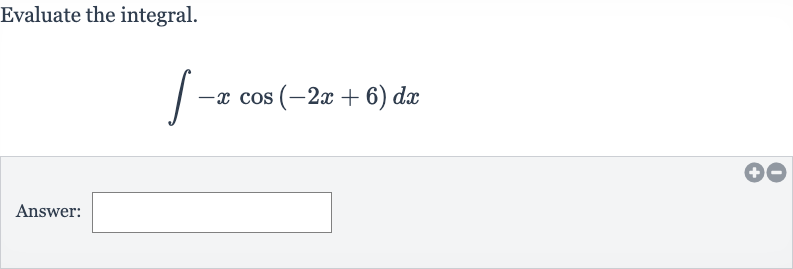
Q. Evaluate the integral.\newline∫−xcos⁡(−2x+6)dx \int-x \cos (-2 x+6) d x \newlineAnswer:
  1. Write Integral: Write down the integral to be solved.\newlineI=∫−xcos⁡(−2x+6) dxI = \int -x \cos(-2x+6)\,dx
  2. Use Substitution: Use substitution to simplify the integral. Let u=−2x+6u = -2x + 6, then du=−2dxdu = -2dx. We need to express dxdx in terms of dudu, so dx=−du2dx = -\frac{du}{2}. Also, when u=−2x+6u = -2x + 6, x=6−u2x = \frac{6 - u}{2}.I=∫−(6−u2)cos⁡(u)(−du2)I = \int -\left(\frac{6 - u}{2}\right) \cos(u) \left(-\frac{du}{2}\right)
  3. Simplify Integral: Simplify the integral by distributing the constants.\newlineI=∫(14)(6−u)cos⁡(u) duI = \int(\frac{1}{4})(6 - u) \cos(u) \, du\newlineI=(14)∫6cos⁡(u) du−(14)∫ucos⁡(u) duI = (\frac{1}{4})\int 6\cos(u) \, du - (\frac{1}{4})\int u\cos(u) \, du
  4. Split and Solve: Split the integral into two parts and solve each part separately.\newlineFirst part: (14)∫6cos⁡(u) du(\frac{1}{4})\int 6\cos(u) \, du\newlineSecond part: −14∫ucos⁡(u) du-\frac{1}{4}\int u\cos(u) \, du
  5. Integrate First Part: Integrate the first part using the basic integral of cos⁡(u)\cos(u).\newlineFirst part: (1/4)∫6cos⁡(u) du=(1/4)(6sin⁡(u))+C1(1/4)\int 6\cos(u) \, du = (1/4)(6\sin(u)) + C_1
  6. Integrate Second Part: Integrate the second part using integration by parts. Let v=uv = u and dw=cos⁡(u)dudw = \cos(u) du. Then dv=dudv = du and w=sin⁡(u)w = \sin(u).
    Second part: -\frac{\(1\)}{\(4\)}\int u\cos(u) du = -\frac{\(1\)}{\(4\)}(u\sin(u) - \int \sin(u) du) = -\frac{\(1\)}{\(4\)}(u\sin(u) + \cos(u)) + C_2
  7. Combine Results: Combine the results from step \(5 and step 66.\newlineI=(14)(6sin⁡(u))−(14)(usin⁡(u)+cos⁡(u))+CI = \left(\frac{1}{4}\right)(6\sin(u)) - \left(\frac{1}{4}\right)(u\sin(u) + \cos(u)) + C
  8. Substitute Back: Substitute back u=−2x+6u = -2x + 6 into the integral.I=14(6sin⁡(−2x+6))−14((−2x+6)sin⁡(−2x+6)+cos⁡(−2x+6))+CI = \frac{1}{4}(6\sin(-2x + 6)) - \frac{1}{4}((-2x + 6)\sin(-2x + 6) + \cos(-2x + 6)) + C
  9. Final Simplification: Simplify the expression. \newlineI=32sin⁡(−2x+6)+12xsin⁡(−2x+6)−14cos⁡(−2x+6)+CI = \frac{3}{2}\sin(-2x + 6) + \frac{1}{2}x\sin(-2x + 6) - \frac{1}{4}\cos(-2x + 6) + C

More problems from Find indefinite integrals using the substitution and by parts

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

View all (114)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant