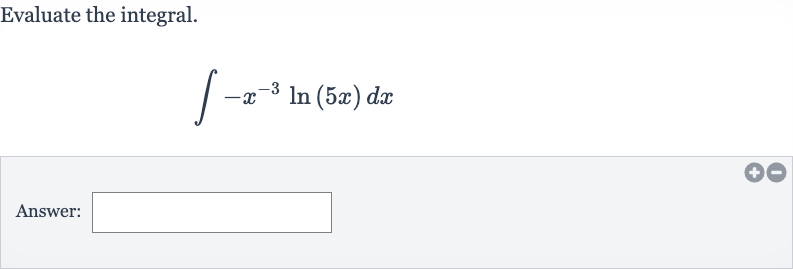
Evaluate the integral. int-x^(-3)ln(5x)dx Answer:

Question

Evaluate the integral.  int-x^(-3)ln(5x)dx Answer:

Bytelearn · Accepted Answer

Recognize Integral Type: Recognize that the integral involves a logarithmic function multiplied by a power of x. This suggests that integration by parts may be a useful technique. The integration by parts formula is ∫u dv = uv - ∫v du.Choose u and dv: Choose u and dv for the integration by parts. Let u = ln(5x) and dv = -x^(-3)dx. Then we need to compute du and v. Differentiating u gives du = (1/x)dx, and integrating dv gives v = (1/2)x^(-2).Compute du and v: Compute du and v. We have du = d(ln(5x))/dx * dx = (1/x)dx and v = ∫-x^(-3)dx = (1/2)x^(-2).Apply Integration by Parts: Apply the integration by parts formula. We have ∫-x^(-3)ln(5x)dx = uv - ∫v du = ln(5x)*(1/2)x^(-2) - ∫(1/2)x^(-2)*(1/x)dx.Simplify Integral: Simplify the integral ∫(1/2)x^(-2)*(1/x)dx. This simplifies to (1/2)∫x^(-3)dx.Integrate Simplified Integral: Integrate (1/2)∫x^(-3)dx. The integral of x^(-3) with respect to x is -1/2 * x^(-2).Combine Integration Results: Combine the results from integration by parts. We have ln(5x)*(1/2)x^(-2) - (1/2)(-1/2 * x^(-2)) = (1/2)x^(-2)ln(5x) + (1/4)x^(-2).Add Constant of Integration: Add the constant of integration C to the result. The final answer is (1/2)x^(-2)ln(5x) + (1/4)x^(-2) + C.

Evaluate the integral. $\newline$ $\int-x^{-3} \ln (5 x) d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫−x−3ln⁡(5x)dx \int-x^{-3} \ln (5 x) d x ∫−x−3ln(5x)dx\newlineAnswer:

Evaluate the integral. $\newline$ $\int-x^{-3} \ln (5 x) d x$ $\newline$ Answer: