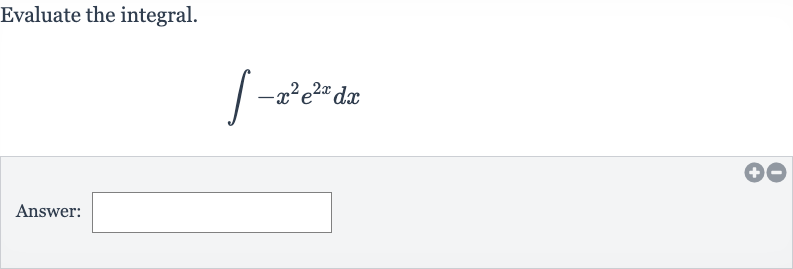
Evaluate the integral. int-x^(2)e^(2x)dx Answer:

Question

Evaluate the integral.  int-x^(2)e^(2x)dx Answer:

Bytelearn · Accepted Answer

Integration by Parts: We will use integration by parts to evaluate the integral of -x^(2)e^(2x) with respect to x. Integration by parts is given by the formula ∫u dv = uv - ∫v du, where u and dv are parts of the integrand that we choose. We will let u = -x^2 (which means du = -2x dx) and dv = e^(2x) dx (which means v = (1/2)e^(2x)). Now we will calculate du and v.Calculate u and v: First, we calculate du by differentiating u = -x^2. The derivative of -x^2 with respect to x is -2x, so du = -2x dx.Apply Integration by Parts: Next, we find v by integrating dv = e^(2x) dx. The integral of e^(2x) with respect to x is (1/2)e^(2x), so v = (1/2)e^(2x).Simplify the Expression: Now we apply the integration by parts formula: ∫u dv = uv - ∫v du. Substituting the values of u, v, and du, we get: ∫-x^2 e^(2x) dx = (-x^2)(1/2)e^(2x) - ∫(1/2)e^(2x)(-2x) dx.Integrate by Parts Again: Simplify the expression: ∫-x^2 e^(2x) dx = (-1/2)x^2 e^(2x) - ∫-x e^(2x) dx.Calculate du and v: We need to integrate -x e^(2x) dx again by parts. Let u = -x (which means du = -dx) and dv = e^(2x) dx (which means v = (1/2)e^(2x)). We calculate du and v again.Apply Integration by Parts Again: Calculate du by differentiating u = -x. The derivative of -x with respect to x is -1, so du = -dx.Simplify the Expression: Find v by integrating dv = e^(2x) dx again. As before, the integral of e^(2x) with respect to x is (1/2)e^(2x), so v = (1/2)e^(2x).Integrate (1/2)e^(2x) dx: Apply the integration by parts formula again: ∫u dv = uv - ∫v du. Substituting the new values of u, v, and du, we get: ∫-x e^(2x) dx = (-x)(1/2)e^(2x) - ∫(1/2)e^(2x)(-1) dx.Combine All Parts: Simplify the expression: ∫-x e^(2x) dx = (-1/2)x e^(2x) + (1/2)∫e^(2x) dx.Final Answer: Now we integrate (1/2)e^(2x) dx. The integral of e^(2x) with respect to x is (1/2)e^(2x), so we get: (1/2)∫e^(2x) dx = (1/2)(1/2)e^(2x) = (1/4)e^(2x).Combine all the parts together to get the final answer: ∫-x^2 e^(2x) dx = (-1/2)x^2 e^(2x) - ((-1/2)x e^(2x) + (1/4)e^(2x)) + C, where C is the constant of integration.Simplify the expression to get the final answer: ∫-x^2 e^(2x) dx = (-1/2)x^2 e^(2x) + (1/2)x e^(2x) - (1/4)e^(2x) + C.

Evaluate the integral. $\newline$ $\int-x^{2} e^{2 x} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫−x2e2xdx \int-x^{2} e^{2 x} d x ∫−x2e2xdx\newlineAnswer:

Evaluate the integral. $\newline$ $\int-x^{2} e^{2 x} d x$ $\newline$ Answer: