AI tutor
Full solution
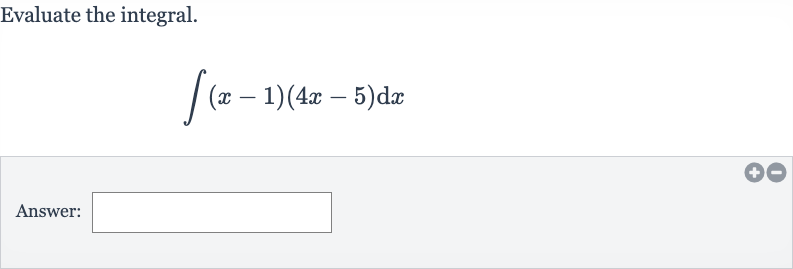
Q. Evaluate the integral.Answer:
- Expand Binomials: Expand the integrand . To integrate the product of two binomials, we first need to expand the expression.
- Write Integral: Write the integral with the expanded integrand.Now we can write the integral as:
- Integrate Separately: Integrate each term separately.The integral of a sum is the sum of the integrals, so we can integrate each term separately.
- Apply Power Rule: Apply the power rule for integration to each term.The power rule states that , where is the constant of integration.
- Combine Integrated Terms: Combine the integrated terms and add the constant of integration.Now we combine all the integrated terms and add the constant of integration .