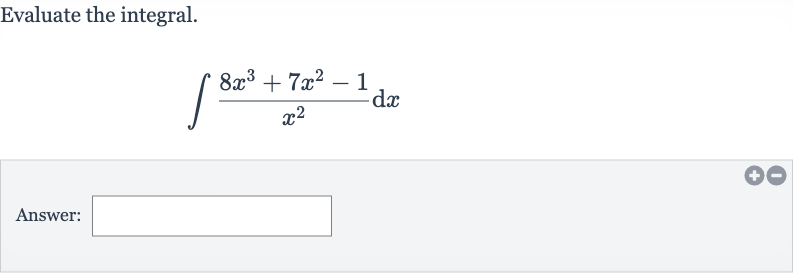AI tutor
Full solution
Q. Evaluate the integral.Answer:
- Simplify integrand: Simplify the integrand by dividing each term by . We have the integral: This simplifies to:
- Integrate each term: Integrate each term separately.The integral of with respect to is .The integral of with respect to is .The integral of with respect to is .So we have:
- Simplify result: Simplify the result from Step .Simplifying the expression, we get:This is the indefinite integral of the given function.