AI tutor
Full solution
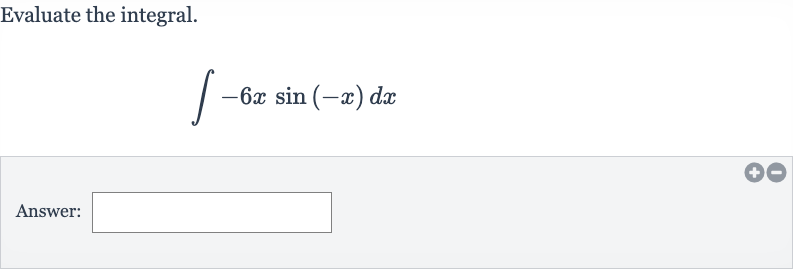
Q. Evaluate the integral.Answer:
- Rewrite Integral: Rewrite the integral by taking the constant outside and using the property .
- Integration by Parts: Apply integration by parts, where and . Then, and . Using the integration by parts formula , we get: \int x \sin(x)dx = x(-\cos(x)) - \int(-\cos(x))(dx) = -x \cos(x) + \int \cos(x)dx
- Integrate Cos: Integrate \(\cos(x) with respect to .
- Substitute Integral: Substitute the integral of back into the equation., where is the constant of integration.
- Final Answer: Write the final answer.The integral of with respect to is .