Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral. int-4x sin(4x+5)dx Answer:

Evaluate the integral.\newline∫−4xsin⁡(4x+5)dx \int-4 x \sin (4 x+5) d x \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitution and by partsright chevron icon

Full solution

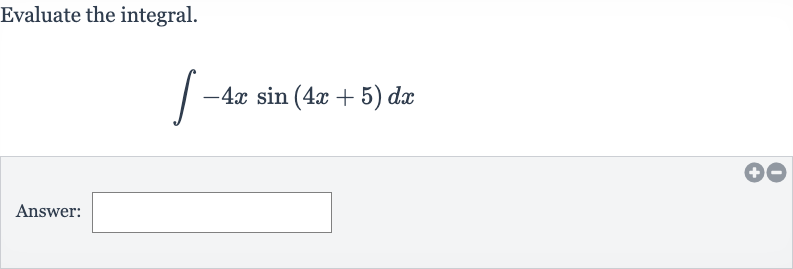
Q. Evaluate the integral.\newline∫−4xsin⁡(4x+5)dx \int-4 x \sin (4 x+5) d x \newlineAnswer:
  1. Choose uu and dvdv: Let's use integration by parts to solve the integral of the form ∫udv\int u dv. We can choose u=−4xu = -4x and dv=sin⁡(4x+5)dxdv = \sin(4x+5)dx. Then we need to find dudu and vv.
    u=−4xu = -4x implies du=−4dxdu = -4 dx
    To find vv, we integrate dvdv:
    dvdv11
    To integrate dvdv22, we use a substitution. Let dvdv33, then dvdv44, or dvdv55.
    dvdv66
    dvdv77
    Now we substitute back dvdv33:
    dvdv99
  2. Integrate dv to find v: Now we apply the integration by parts formula:\newline∫udv=uv−∫vdu\int u dv = uv - \int v du\newlinePlugging in our uu, vv, dudu, and dvdv, we get:\newline∫(−4x)sin⁡(4x+5)dx=−4x⋅(−14cos⁡(4x+5))−∫(−14cos⁡(4x+5))⋅(−4)dx\int (-4x) \sin(4x+5)dx = -4x \cdot \left(-\frac{1}{4}\cos(4x+5)\right) - \int \left(-\frac{1}{4}\cos(4x+5)\right) \cdot (-4)dx\newlineSimplify the equation:\newline∫(−4x)sin⁡(4x+5)dx=xcos⁡(4x+5)−∫cos⁡(4x+5)dx\int (-4x) \sin(4x+5)dx = x\cos(4x+5) - \int \cos(4x+5)dx
  3. Apply integration by parts formula: Now we need to integrate cos⁡(4x+5)\cos(4x+5). We will use the same substitution as before:\newlinew=4x+5w = 4x+5, dw=4 dxdw = 4\,dx, or dx=dw4dx = \frac{dw}{4}.\newline∫cos⁡(4x+5) dx=∫cos⁡(w)⋅(14)dw\int \cos(4x+5)\,dx = \int \cos(w) \cdot \left(\frac{1}{4}\right)dw\newlineThis integral is straightforward:\newline∫cos⁡(w)⋅(14)dw=(14)sin⁡(w)\int \cos(w) \cdot \left(\frac{1}{4}\right)dw = \left(\frac{1}{4}\right)\sin(w)\newlineSubstitute back w=4x+5w = 4x+5:\newline∫cos⁡(4x+5) dx=(14)sin⁡(4x+5)\int \cos(4x+5)\,dx = \left(\frac{1}{4}\right)\sin(4x+5)
  4. Integrate cos⁡(4x+5)\cos(4x+5): Now we substitute the integral we just found back into our integration by parts formula:\newline∫(−4x)sin⁡(4x+5) dx=xcos⁡(4x+5)−(14)sin⁡(4x+5)\int(-4x) \sin(4x+5)\,dx = x\cos(4x+5) - (\frac{1}{4})\sin(4x+5)\newlineThis is the antiderivative of the function. We add the constant of integration CC to complete the indefinite integral.

More problems from Find indefinite integrals using the substitution and by parts

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

View all (114)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant