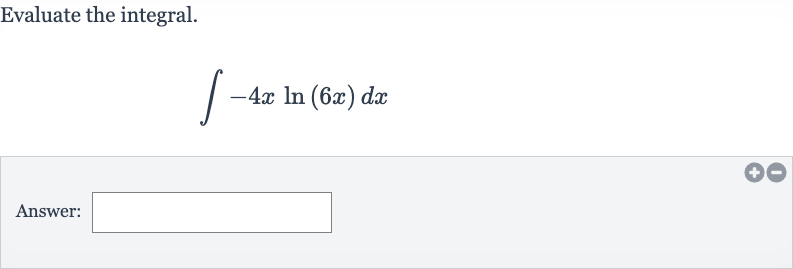
Evaluate the integral. int-4x ln(6x)dx Answer:

Question

Evaluate the integral.  int-4x ln(6x)dx Answer:

Bytelearn · Accepted Answer

Choose u and dv: Let's use integration by parts to solve the integral $\int -4x \ln(6x) \, dx$. Integration by parts is given by the formula $\int u \, dv = uv - \int v \, du$, where $u$ and $dv$ are parts of the integrand we choose to differentiate and integrate, respectively.  Choose $u = \ln(6x)$ and $dv = -4x \, dx$. Then we need to compute $du$ and $v$.  Differentiate $u$ to get $du$: $du = \frac{d}{dx} \ln(6x) \, dx = \frac{1}{6x} \cdot 6 \, dx = dx$.  Integrate $dv$ to get $v$: $v = \int -4x \, dx = -2x^2$.  Now we have $u$, $dv$, $du$, and $v$.Apply integration by parts: Apply the integration by parts formula: $\int -4x \ln(6x) \, dx = uv - \int v \, du$.  Substitute the values of $u$, $dv$, $du$, and $v$ into the formula: $\int -4x \ln(6x) \, dx = \ln(6x) \cdot (-2x^2) - \int -2x^2 \, dx$.  Now we need to integrate $-2x^2$.Integrate dv to get v: Integrate $-2x^2$ with respect to $x$: $\int -2x^2 \, dx = -\frac{2}{3}x^3 + C$, where $C$ is the constant of integration.  Now we can write the full expression for the integral: $\int -4x \ln(6x) \, dx = -2x^2 \ln(6x) - \left(-\frac{2}{3}x^3 + C\right)$.  Simplify the expression: $\int -4x \ln(6x) \, dx = -2x^2 \ln(6x) + \frac{2}{3}x^3 + C$.

Evaluate the integral. $\newline$ $\int-4 x \ln (6 x) d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫−4xln⁡(6x)dx \int-4 x \ln (6 x) d x ∫−4xln(6x)dx\newlineAnswer:

Evaluate the integral. $\newline$ $\int-4 x \ln (6 x) d x$ $\newline$ Answer: