AI tutor
Full solution
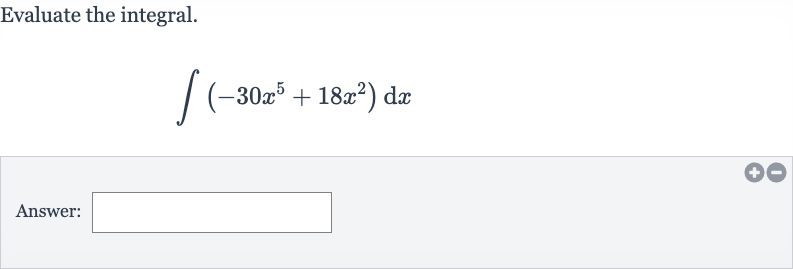
Q. Evaluate the integral.Answer:
- Given Integral: We are given the integral to evaluate: We will integrate the function term by term.
- Integrating : First, we integrate the term with respect to . The antiderivative of is , so the antiderivative of is: Simplifying, we get:
- Integrating : Next, we integrate the term with respect to . The antiderivative of is , so the antiderivative of is: Simplifying, we get:
- Combining Results: Now, we combine the results of the two integrals and add the constant of integration . The final indefinite integral is: