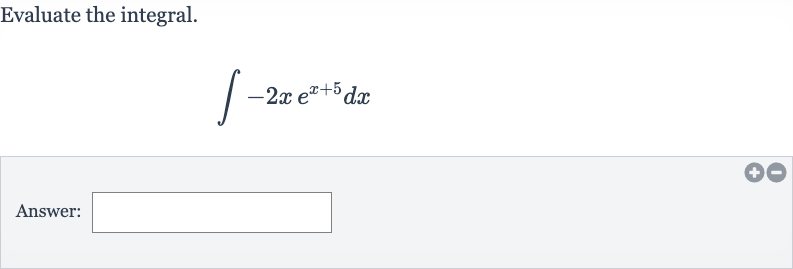
Evaluate the integral. int-2xe^(x+5)dx Answer:

Question

Evaluate the integral.  int-2xe^(x+5)dx Answer:

Bytelearn · Accepted Answer

Identify Integral: Let's start by identifying the integral we need to evaluate: I = ∫-2xe^(x+5)dx This is an integration problem that can be solved using integration by parts, which is based on the formula ∫udv = uv - ∫vdu, where u and dv are parts of the integrand chosen such that du and v can be easily computed.Choose u and dv: Choose u and dv for the integration by parts. Let's let u = -2x, which means du = -2dx. Let dv = e^(x+5)dx, which means v is the antiderivative of e^(x+5), which is e^(x+5) itself since the derivative of e^(x+5) is e^(x+5).Apply Integration by Parts: Now we apply the integration by parts formula: ∫-2xe^(x+5)dx = uv - ∫vdu = (-2x)e^(x+5) - ∫e^(x+5)(-2dx)Simplify Integral: Simplify the integral: = -2xe^(x+5) + 2∫e^(x+5)dx Now we need to integrate e^(x+5) with respect to x, which is straightforward since the integral of e^(x+5) is e^(x+5).Perform Integration: Perform the integration: 2∫e^(x+5)dx = 2e^(x+5) So the integral becomes: -2xe^(x+5) + 2e^(x+5)Combine Terms: Combine the terms to get the final answer: I = -2xe^(x+5) + 2e^(x+5) + C where C is the constant of integration.

Evaluate the integral. $\newline$ $\int-2 x e^{x+5} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫−2xex+5dx \int-2 x e^{x+5} d x ∫−2xex+5dx\newlineAnswer:

Evaluate the integral. $\newline$ $\int-2 x e^{x+5} d x$ $\newline$ Answer: