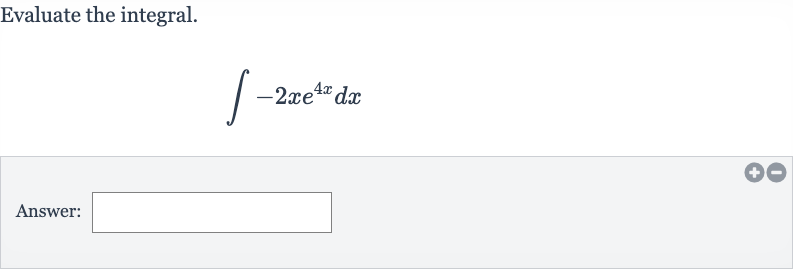
Evaluate the integral. int-2xe^(4x)dx Answer:

Question

Evaluate the integral.  int-2xe^(4x)dx Answer:

Bytelearn · Accepted Answer

Identify integral: Identify the integral that needs to be evaluated. The integral to be evaluated is ∫-2xe^(4x)dx.Recognize form: Recognize that the integral is in the form suitable for integration by parts. Integration by parts is given by the formula ∫u dv = uv - ∫v du, where u and dv are parts of the integrand.Choose u and dv: Choose u and dv. Let u = -2x, which implies du = -2dx. Let dv = e^(4x)dx, which implies v = (1/4)e^(4x) after integrating dv.Apply integration by parts: Apply the integration by parts formula. Using the integration by parts formula, we get: ∫-2xe^(4x)dx = uv - ∫v du = (-2x)(1/4)e^(4x) - ∫(1/4)e^(4x)(-2dx) = (-1/2)xe^(4x) + (1/2)∫e^(4x)dxIntegrate remaining integral: Integrate the remaining integral. The remaining integral is ∫e^(4x)dx, which is (1/4)e^(4x) after integration.Substitute result: Substitute the result of the integration back into the equation. Substituting the result from Step 5 into the equation from Step 4, we get: ∫-2xe^(4x)dx = (-1/2)xe^(4x) + (1/2)((1/4)e^(4x)) + C = (-1/2)xe^(4x) + (1/8)e^(4x) + CCombine final answer: Combine like terms and write the final answer. The final answer is: ∫-2xe^(4x)dx = (-1/2)xe^(4x) + (1/8)e^(4x) + C

Evaluate the integral. $\newline$ $\int-2 x e^{4 x} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫−2xe4xdx \int-2 x e^{4 x} d x ∫−2xe4xdx\newlineAnswer:

Evaluate the integral. $\newline$ $\int-2 x e^{4 x} d x$ $\newline$ Answer: