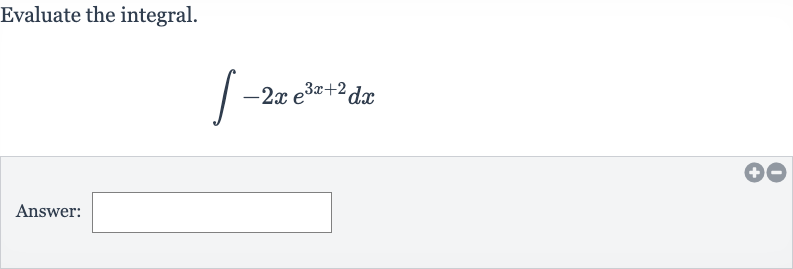
Evaluate the integral. int-2xe^(3x+2)dx Answer:

Question

Evaluate the integral.  int-2xe^(3x+2)dx Answer:

Bytelearn · Accepted Answer

Identify Integral: Let's start by identifying the integral we need to evaluate: I = ∫-2xe^(3x+2)dx We can use integration by parts, which states that ∫u dv = uv - ∫v du, where u and dv are parts of the integrand we choose to differentiate and integrate, respectively. Let's choose u = -2x (which will be differentiated) and dv = e^(3x+2)dx (which will be integrated).Choose u and dv: Differentiate u with respect to x to find du: u = -2x du/dx = -2 du = -2dxDifferentiate u: Integrate dv with respect to x to find v: dv = e^(3x+2)dx To integrate e^(3x+2), we need to use the substitution method. Let w = 3x+2, then dw/dx = 3, dx = dw/3. v = ∫e^(3x+2)dx = ∫e^w * (dw/3) = (1/3)e^w + C Substitute back w = 3x+2: v = (1/3)e^(3x+2)Integrate dv: Now apply the integration by parts formula: I = uv - ∫v du I = (-2x)(1/3)e^(3x+2) - ∫(1/3)e^(3x+2)(-2dx) I = (-2/3)xe^(3x+2) + (2/3)∫e^(3x+2)dxApply Integration by Parts: We have already found the integral of e^(3x+2)dx when we calculated v, so we can use that result: I = (-2/3)xe^(3x+2) + (2/3)((1/3)e^(3x+2)) + C I = (-2/3)xe^(3x+2) + (2/9)e^(3x+2) + CUse Result for Integral: Combine the terms with the common factor e^(3x+2): I = e^(3x+2)((-2/3)x + (2/9)) + CCombine Terms: Simplify the expression inside the parentheses: I = e^(3x+2)((-6/9)x + (2/9)) + C I = e^(3x+2)((-6x + 2)/9) + CSimplify Expression: Factor out the common factor of 1/9: I = (1/9)e^(3x+2)(-6x + 2) + C

Evaluate the integral. $\newline$ $\int-2 x e^{3 x+2} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫−2xe3x+2dx \int-2 x e^{3 x+2} d x ∫−2xe3x+2dx\newlineAnswer:

Evaluate the integral. $\newline$ $\int-2 x e^{3 x+2} d x$ $\newline$ Answer: