AI tutor
Full solution
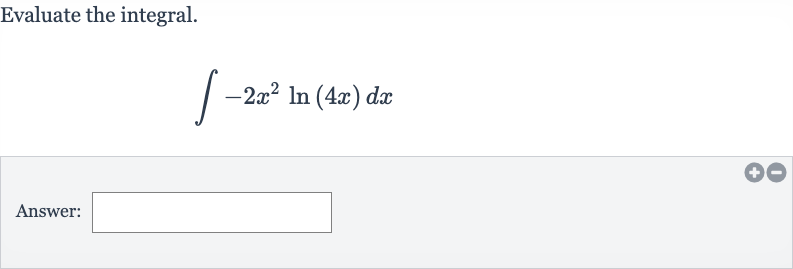
Q. Evaluate the integral.Answer:
- Identify integral: Identify the integral to be solved.We need to evaluate the integral of the function with respect to .
- Apply integration by parts: Apply integration by parts. Integration by parts formula is . Let and . Then we need to find and . and .
- Calculate : Calculate .
- Apply integration by parts formula: Apply the integration by parts formula.
- Integrate remaining term: Integrate the remaining term.
- Substitute integral: Substitute the integral into the equation.
- Add constant of integration: Add the constant of integration.