AI tutor
Full solution
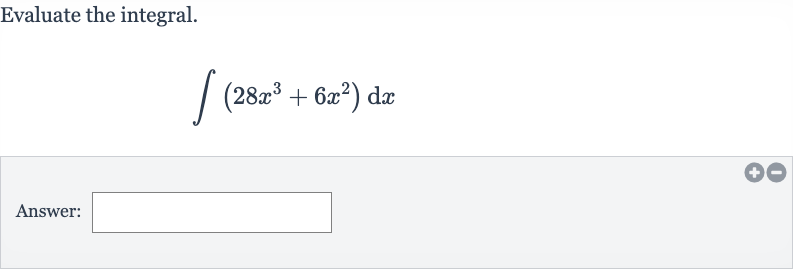
Q. Evaluate the integral.Answer:
- Given integral: We are given the integral to evaluate: We will integrate term by term.
- Integrating : The integral of with respect to is:
- Integrating : The integral of with respect to is:
- Adding integrals and constant: Now we add the two integrals together and include the constant of integration :