AI tutor
Full solution
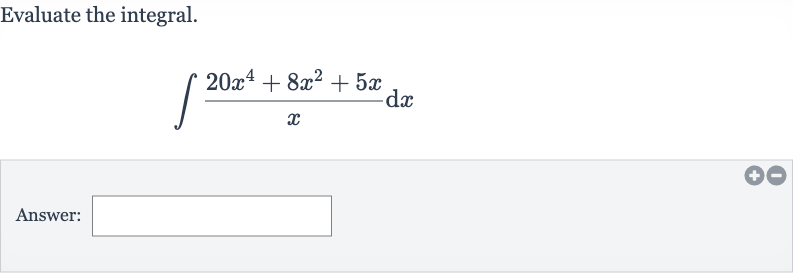
Q. Evaluate the integral.Answer:
- Given Integral Simplification: We are given the integral: First, we simplify the integrand by dividing each term by .
- Integrating Each Term: Now we integrate each term separately. For the first term, the integral of is , so:For the second term:For the third term:
- Combining Integrals: Now we combine the results of the integrals.Simplify each term:
- Adding Constant of Integration: Finally, we add the constant of integration to the result.