AI tutor
Full solution
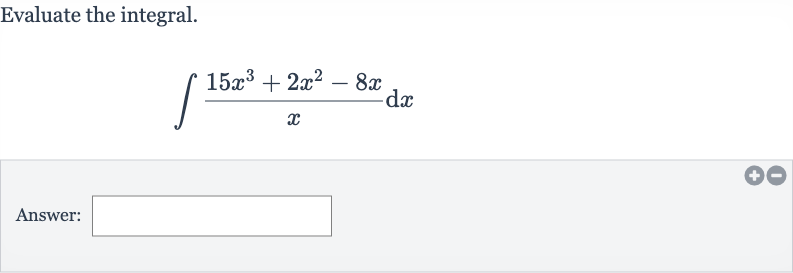
Q. Evaluate the integral.Answer:
- Simplify integrand: Simplify the integrand by dividing each term by .
- Integrate each term: Integrate each term separately.=
- Calculate integrals: Calculate the integral of each term.
- Combine results: Combine the results and add the constant of integration .