Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral and express your answer in simplest form. int(10)/(sqrt(16-4x^(2)))dx Answer:

Evaluate the integral and express your answer in simplest form.\newline∫1016−4x2dx \int \frac{10}{\sqrt{16-4 x^{2}}} d x \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitutionright chevron icon

Full solution

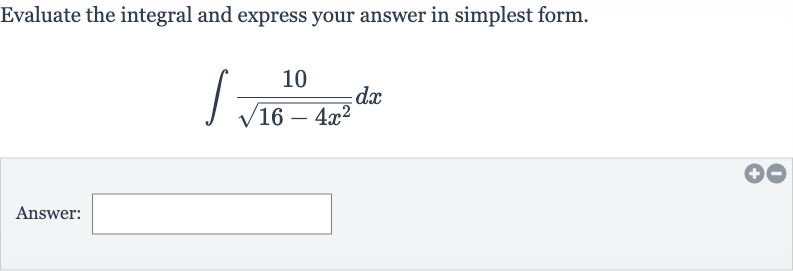
Q. Evaluate the integral and express your answer in simplest form.\newline∫1016−4x2dx \int \frac{10}{\sqrt{16-4 x^{2}}} d x \newlineAnswer:
  1. Substitution: We are given the integral: \newline∫1016−4x2dx\int \frac{10}{\sqrt{16-4x^{2}}}dx\newlineTo solve this integral, we can use a trigonometric substitution. Let's choose x=2sin⁡(θ)x = 2\sin(\theta), because the expression under the square root resembles the Pythagorean identity 1−sin⁡2(θ)=cos⁡2(θ)1 - \sin^{2}(\theta) = \cos^{2}(\theta). This will simplify the square root.
  2. Differentiation: First, we need to find dxdx in terms of d(θ)d(\theta). Differentiating x=2sin⁡(θ)x = 2\sin(\theta) with respect to θ\theta gives us:\newlinedxd(θ)=2cos⁡(θ)\frac{dx}{d(\theta)} = 2\cos(\theta)\newlineTherefore, dx=2cos⁡(θ)d(θ)dx = 2\cos(\theta)d(\theta)
  3. Integral Substitution: Now, we substitute x=2sin⁡(θ)x = 2\sin(\theta) and dx=2cos⁡(θ)d(θ)dx = 2\cos(\theta)d(\theta) into the integral:\newline∫1016−4x2dx=∫1016−4(2sin⁡(θ))2⋅2cos⁡(θ)d(θ)\int\frac{10}{\sqrt{16-4x^{2}}}dx = \int\frac{10}{\sqrt{16-4(2\sin(\theta))^2}} \cdot 2\cos(\theta)d(\theta)\newlineSimplify the expression under the square root:\newline∫1016−4(4sin⁡2(θ))⋅2cos⁡(θ)d(θ)=∫1016−16sin⁡2(θ)⋅2cos⁡(θ)d(θ)\int\frac{10}{\sqrt{16-4(4\sin^2(\theta))}} \cdot 2\cos(\theta)d(\theta) = \int\frac{10}{\sqrt{16-16\sin^2(\theta)}} \cdot 2\cos(\theta)d(\theta)
  4. Simplify Expression: The expression under the square root simplifies to 16cos⁡2(θ)16\cos^2(\theta), using the Pythagorean identity:\newline∫(1016−16sin⁡2(θ))⋅2cos⁡(θ)d(θ)=∫(1016cos⁡2(θ))⋅2cos⁡(θ)d(θ)\int(\frac{10}{\sqrt{16-16\sin^2(\theta)}}) \cdot 2\cos(\theta)d(\theta) = \int(\frac{10}{\sqrt{16\cos^2(\theta)}}) \cdot 2\cos(\theta)d(\theta)\newlineSimplify the square root:\newline∫(104cos⁡(θ))⋅2cos⁡(θ)d(θ)=∫(104⋅2cos⁡(θ)cos⁡(θ))d(θ)\int(\frac{10}{4\cos(\theta)}) \cdot 2\cos(\theta)d(\theta) = \int(\frac{10}{4} \cdot \frac{2\cos(\theta)}{\cos(\theta)})d(\theta)
  5. Integrate with Respect: The cos⁡(θ)\cos(\theta) terms cancel out, leaving us with:\newline∫(104⋅2)d(θ)=∫(5)d(θ)\int(\frac{10}{4} \cdot 2)d(\theta) = \int(5)d(\theta)\newlineNow, integrate with respect to theta:\newline∫(5)d(θ)=5θ+C\int(5)d(\theta) = 5\theta + C
  6. Final Answer: We need to express the answer in terms of xx, so we have to substitute back for θ\theta using our original substitution x=2sin⁡(θ)x = 2\sin(\theta). To find θ\theta, we use the inverse sine function:\newlineθ=arcsin⁡(x2)\theta = \arcsin(\frac{x}{2})\newlineSo the integral in terms of xx is:\newline5θ+C=5arcsin⁡(x2)+C5\theta + C = 5\arcsin(\frac{x}{2}) + C

More problems from Find indefinite integrals using the substitution

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

View all (263)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant