Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral and express your answer in simplest form. int(-1)/(sqrt(25-9x^(2)))dx Answer:

Evaluate the integral and express your answer in simplest form.\newline∫−125−9x2dx \int \frac{-1}{\sqrt{25-9 x^{2}}} d x \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitutionright chevron icon

Full solution

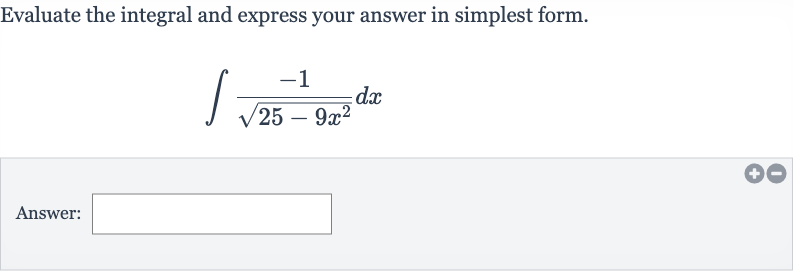
Q. Evaluate the integral and express your answer in simplest form.\newline∫−125−9x2dx \int \frac{-1}{\sqrt{25-9 x^{2}}} d x \newlineAnswer:
  1. Given Integral: We are given the integral: \newline∫−125−9x2dx\int \frac{-1}{\sqrt{25-9x^{2}}}dx\newlineTo solve this integral, we can use a trigonometric substitution. Let's choose x=53sin⁡(θ)x = \frac{5}{3}\sin(\theta), because the expression 25−9x225 - 9x^2 resembles a Pythagorean identity when xx is expressed in terms of sine.
  2. Trigonometric Substitution: Differentiate x=53sin⁡(θ)x = \frac{5}{3}\sin(\theta) with respect to θ\theta to find dxdx:dxdθ=53cos⁡(θ)\frac{dx}{d\theta} = \frac{5}{3}\cos(\theta)dx=53cos⁡(θ)dθdx = \frac{5}{3}\cos(\theta)d\theta
  3. Differentiate xx: Substitute x=53sin⁡(θ)x = \frac{5}{3}\sin(\theta) and dx=53cos⁡(θ)dθdx = \frac{5}{3}\cos(\theta)d\theta into the integral:\newline∫−125−9x2dx=∫−125−9(53)2sin⁡2(θ)(53)cos⁡(θ)dθ\int \frac{-1}{\sqrt{25-9x^{2}}}dx = \int \frac{-1}{\sqrt{25-9\left(\frac{5}{3}\right)^2\sin^2(\theta)}}\left(\frac{5}{3}\right)\cos(\theta)d\theta\newlineSimplify the expression inside the square root:\newline25−9(53)2sin⁡2(θ)=25−25sin⁡2(θ)=25(1−sin⁡2(θ))25 - 9\left(\frac{5}{3}\right)^2\sin^2(\theta) = 25 - 25\sin^2(\theta) = 25(1 - \sin^2(\theta))
  4. Substitute xx and dxdx: Recognize that 1−sin⁡2(θ)1 - \sin^2(\theta) is equal to cos⁡2(θ)\cos^2(\theta) by the Pythagorean identity:\newline25(1−sin⁡2(θ))=25cos⁡2(θ)25(1 - \sin^2(\theta)) = 25\cos^2(\theta)\newlineNow, substitute this back into the integral:\newline∫(−1)/(25−9∗(5/3)2sin⁡2(θ))∗(5/3)cos⁡(θ)dθ=∫(−1)/(25cos⁡2(θ))∗(5/3)cos⁡(θ)dθ\int(-1)/(\sqrt{25-9*(5/3)^2\sin^2(\theta)})*(5/3)\cos(\theta)d\theta = \int(-1)/(\sqrt{25\cos^2(\theta)})*(5/3)\cos(\theta)d\theta
  5. Simplify Expression: Simplify the integral by taking the square root of 25cos⁡2(θ)25\cos^2(\theta), which is 5cos⁡(θ)5\cos(\theta):\newline∫−15cos⁡(θ)(53cos⁡(θ))dθ\int\frac{-1}{5\cos(\theta)}\left(\frac{5}{3}\cos(\theta)\right)d\theta\newlineThe cos⁡(θ)\cos(\theta) terms cancel out, and we are left with:\newline∫(−13)dθ\int\left(-\frac{1}{3}\right)d\theta
  6. Recognize Identity: Integrate −13-\frac{1}{3} with respect to θ\theta:∫(−13)dθ=−13×θ+C\int\left(-\frac{1}{3}\right)d\theta = -\frac{1}{3} \times \theta + C
  7. Simplify Integral: Now we need to express θ\theta back in terms of xx. Since x=53sin⁡(θ)x = \frac{5}{3}\sin(\theta), we can solve for θ\theta using the inverse sine function:\newlinesin⁡(θ)=35x\sin(\theta) = \frac{3}{5}x\newlineθ=arcsin⁡(35x)\theta = \arcsin(\frac{3}{5}x)\newlineSubstitute θ\theta back into the integral result:\newline−13⋅θ+C=−13⋅arcsin⁡(35x)+C-\frac{1}{3} \cdot \theta + C = -\frac{1}{3} \cdot \arcsin(\frac{3}{5}x) + C

More problems from Find indefinite integrals using the substitution

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

View all (263)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant