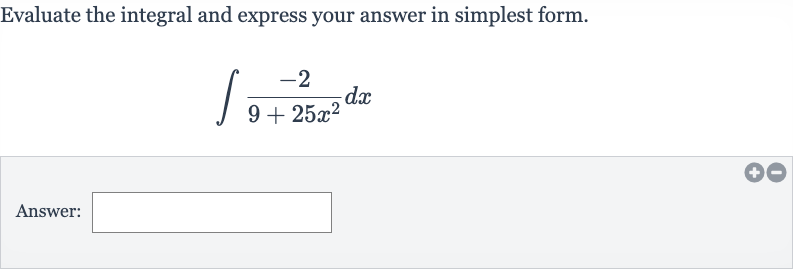Evaluate the integral and express your answer in simplest form. int(-2)/(9+25x^(2))dx Answer:

Question

Evaluate the integral and express your answer in simplest form.  int(-2)/(9+25x^(2))dx Answer:

Bytelearn · Accepted Answer

Recognize Integral Form: We are given the integral to evaluate: int(-2)/(9+25x^(2))dx First, we notice that the denominator can be written as a sum of squares, which suggests a trigonometric substitution. However, we can also use a direct substitution if we recognize that the integral is in the form of an arctangent function. We will use the substitution method.Substitution with u: Let's make the substitution u = 5x, which means du = 5dx. We need to express dx in terms of du, so we get dx = du/5.Factor Out Constants: Now we substitute 5x with u and dx with du/5 in the integral: int(-2)/(9+25x^(2))dx = int(-2)/(9+u^(2)) * (du/5) We can factor out constants from the integral: = (-2/5) * int(1)/(9+u^(2))duUse Integral Formula: The integral of 1/(a^2 + u^2) is (1/a) * arctan(u/a) + C, where a is a constant. In our case, a^2 = 9, so a = 3. We can now integrate using this formula: (-2/5) * int(1)/(9+u^(2))du = (-2/5) * (1/3) * arctan(u/3) + CSimplify Constant Factors: Simplify the constant factors: (-2/5) * (1/3) = -2/15 So the integral becomes: -2/15 * arctan(u/3) + CSubstitute Back u: Now we substitute back u = 5x to get the integral in terms of x: -2/15 * arctan(5x/3) + CFinal Indefinite Integral: We have found the indefinite integral in its simplest form: int(-2)/(9+25x^(2))dx = -2/15 * arctan(5x/3) + C

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{-2}{9+25 x^{2}} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Evaluate the integral and express your answer in simplest form.\newline∫−29+25x2dx \int \frac{-2}{9+25 x^{2}} d x ∫9+25x2−2​dx\newlineAnswer:

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{-2}{9+25 x^{2}} d x$ $\newline$ Answer: