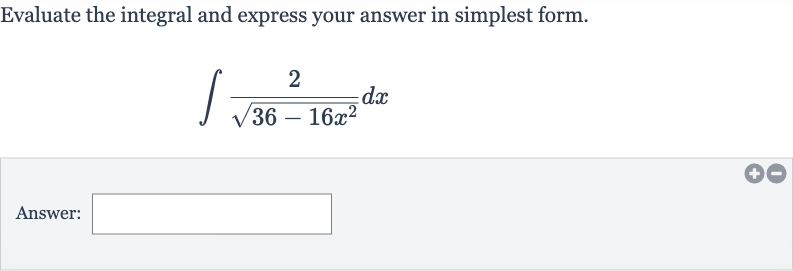
Evaluate the integral and express your answer in simplest form. int(2)/(sqrt(36-16x^(2)))dx Answer:

Question

Evaluate the integral and express your answer in simplest form.  int(2)/(sqrt(36-16x^(2)))dx Answer:

Bytelearn · Accepted Answer

Recognize inverse trigonometric function: Recognize the integral as a form of the inverse trigonometric function. The integral resembles the form of the inverse sine function, which has the integral formula int(1/sqrt(a^2 - u^2))du = arcsin(u/a) + C, where a is a constant. In this case, we can try to match the integral to this form by factoring out constants from the square root.Factor out constant from square root: Factor out the constant from the square root to match the inverse sine integral form. int(2)/(sqrt(36-16x^(2)))dx = int(2)/(sqrt(4^2(9-x^(2))))dx Now, factor out the 4^2 from under the square root to get: int(2)/(4sqrt(9-x^(2)))dx = int(1)/(2sqrt(9-x^(2)))dxSubstitute u to transform integral: Substitute u = x/3 to transform the integral into the standard form. Let u = x/3, then du = (1/3)dx, and dx = 3du. Substitute x = 3u into the integral: int(1)/(2sqrt(9-(3u)^(2))) * 3du = int(3)/(2sqrt(9-9u^(2)))du Simplify the integral: int(3)/(2sqrt(9(1-u^(2))))du = int(3)/(6sqrt(1-u^(2)))du = int(1)/(2sqrt(1-u^(2)))duIntegrate using inverse sine function: Integrate using the inverse sine function. The integral is now in the standard form for the inverse sine function: int(1)/(2sqrt(1-u^(2)))du = (1/2)arcsin(u) + CSubstitute back original variable: Substitute back the original variable x into the integral. Since u = x/3, we substitute back to get the final answer: (1/2)arcsin(x/3) + C

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{2}{\sqrt{36-16 x^{2}}} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Evaluate the integral and express your answer in simplest form.\newline∫236−16x2dx \int \frac{2}{\sqrt{36-16 x^{2}}} d x ∫36−16x2​2​dx\newlineAnswer:

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{2}{\sqrt{36-16 x^{2}}} d x$ $\newline$ Answer: