AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Evaluate the integral and express your answer in simplest form.Answer:
Full solution
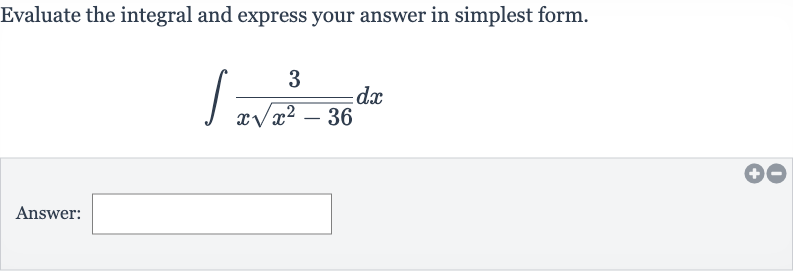
Q. Evaluate the integral and express your answer in simplest form.Answer:
- Recognize integral form: Let's start by recognizing that the integral resembles the form of the derivative of an inverse trigonometric function, specifically the inverse hyperbolic function. We can use a substitution to simplify the integral. Let's set , which implies . When , , and as approaches infinity, approaches . The integral becomes:
- Simplify with substitution: Simplify the integral by substituting and := = = = = =
- Integrate secant function: Now we integrate :\int(\frac{\(1\)}{\(6\)})\sec(\theta)d\theta = (\frac{\(1\)}{\(6\)})\ln|\sec(\theta) + \tan(\theta)| + C
- Back-substitute for x: We need to back-substitute to return to the original variable x. From our substitution, we have \(x = 6\sec(\theta), so . Also, . Therefore, the integral in terms of x is:\frac{\(1\)}{\(6\)}\ln|\sec(\theta) + \tan(\theta)| + C\(\newline= \frac{}{}\ln|\left(\frac{x}{}\right) + \left(\frac{\sqrt{x^}}{}\right)| + C= \frac{}{}\ln|\frac{x + \sqrt{x^}}{}| + C= \frac{}{}\ln|x + \sqrt{x^}| - \frac{}{}\ln() + C
- Combine constant terms: We can combine the constant terms into a single constant of integration:(\frac{1}{6})\ln|x + \sqrt{(x^2-36)}| - (\frac{1}{6})\ln(6) + C\(\newline= (\frac{1}{6})\ln|x + \sqrt{(x^2-36)}| - \ln(6^{(\frac{1}{6})}) + C= (\frac{1}{6})\ln|x + \sqrt{(x^2-36)}| + C'\)where is a new constant of integration that absorbs the term.
