Full solution
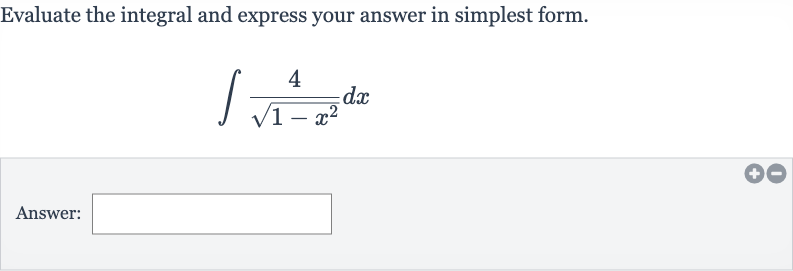
Q. Evaluate the integral and express your answer in simplest form.Answer:
- Given Integral: We are given the integral:This integral is a standard form that resembles the integral of the derivative of arcsine, which is:To solve the given integral, we can factor out the constant from the integral:
- Factor Out Constant: Now we can integrate using the standard form:where is the constant of integration.
- Integrate Using Standard Form: Therefore, the integral evaluates to:This is the simplest form of the answer.