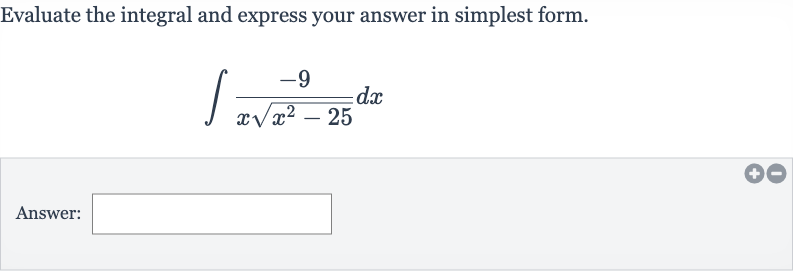
Evaluate the integral and express your answer in simplest form. int(-9)/(xsqrt(x^(2)-25))dx Answer:

Question

Evaluate the integral and express your answer in simplest form.  int(-9)/(xsqrt(x^(2)-25))dx Answer:

Bytelearn · Accepted Answer

Identify Integral: Let's identify the integral we need to evaluate: I = ∫(-9)/(x*sqrt(x^2-25)) dx To solve this integral, we can use a trigonometric substitution. Let x = 5sec(θ), which implies dx = 5sec(θ)tan(θ) dθ. When x = 5sec(θ), sqrt(x^2-25) becomes sqrt(25sec^2(θ)-25) = 5tan(θ).Trigonometric Substitution: Substitute x = 5sec(θ) and dx = 5sec(θ)tan(θ) dθ into the integral: I = ∫(-9)/(5sec(θ)*5tan(θ)) * 5sec(θ)tan(θ) dθ Simplify the integral: I = ∫(-9)/5 dθSubstitute and Simplify: Integrate with respect to θ: I = (-9/5)θ + C, where C is the constant of integration.Integrate with Respect: Now we need to express θ in terms of x to get back to the original variable. From x = 5sec(θ), we have sec(θ) = x/5. Taking the arccosine of both sides, we get θ = sec^(-1)(x/5).Express in Terms of x: Substitute θ back into the integral result: I = (-9/5)sec^(-1)(x/5) + C This is the simplest form of the integral in terms of x.

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{-9}{x \sqrt{x^{2}-25}} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral and express your answer in simplest form.\newline∫−9xx2−25dx \int \frac{-9}{x \sqrt{x^{2}-25}} d x ∫xx2−25​−9​dx\newlineAnswer:

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{-9}{x \sqrt{x^{2}-25}} d x$ $\newline$ Answer: