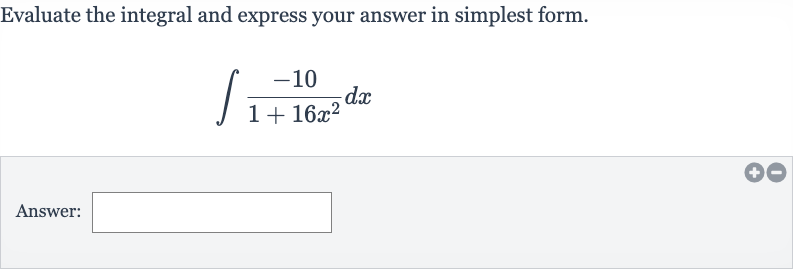Evaluate the integral and express your answer in simplest form. int(-10)/(1+16x^(2))dx Answer:

Question

Evaluate the integral and express your answer in simplest form.  int(-10)/(1+16x^(2))dx Answer:

Bytelearn · Accepted Answer

Recognize standard form: Recognize the integral as a standard form. The integral int(-10)/(1+16x^(2))dx resembles the standard form of the integral for arctangent, int(1)/(a^2 + x^2)dx = (1/a)arctan(x/a) + C, where a is a constant.Factor out constant: Factor out the constant from the integral. Factor out the constant -10 from the integral to simplify the expression. int(-10)/(1+16x^(2))dx = -10 * int(1)/(1+16x^(2))dxIdentify 'a': Identify the value of 'a' in the standard form. In the standard form (1/a)arctan(x/a) + C, we need to match the denominator 1+16x^2 with a^2+x^2. Here, a^2 = 1/16, so a = 1/4.Apply arctangent integral: Apply the standard form of the arctangent integral. Using the standard form, we can rewrite the integral as: -10 * int(1)/(1+16x^(2))dx = -10 * (1/(4))arctan(x/(1/4)) + CSimplify expression: Simplify the expression. Simplify the expression by multiplying the constants. -10 * (1/(4))arctan(x/(1/4)) + C = (-10/4)arctan(4x) + C = -2.5arctan(4x) + C

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{-10}{1+16 x^{2}} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Evaluate the integral and express your answer in simplest form.\newline∫−101+16x2dx \int \frac{-10}{1+16 x^{2}} d x ∫1+16x2−10​dx\newlineAnswer:

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{-10}{1+16 x^{2}} d x$ $\newline$ Answer: