Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral and express your answer in simplest form. int(-7)/(sqrt(16-4x^(2)))dx Answer:

Evaluate the integral and express your answer in simplest form.\newline∫−716−4x2dx \int \frac{-7}{\sqrt{16-4 x^{2}}} d x \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitutionright chevron icon

Full solution

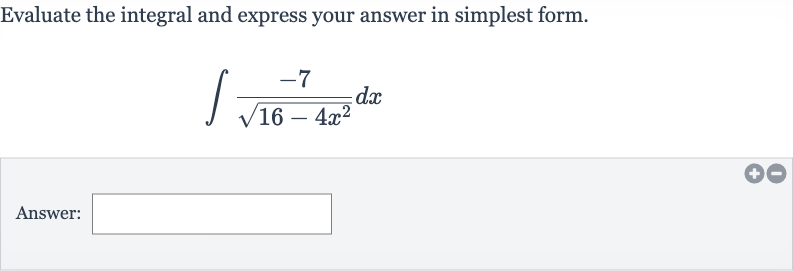
Q. Evaluate the integral and express your answer in simplest form.\newline∫−716−4x2dx \int \frac{-7}{\sqrt{16-4 x^{2}}} d x \newlineAnswer:
  1. Choose Trig Substitution: We are given the integral: \newline∫−716−4x2dx\int \frac{-7}{\sqrt{16-4x^{2}}}dx\newlineTo solve this integral, we can use a trigonometric substitution. Let's choose x=2sin⁡(θ)x = 2\sin(\theta), because the expression under the square root resembles the Pythagorean identity 1−sin⁡2(θ)=cos⁡2(θ)1 - \sin^{2}(\theta) = \cos^{2}(\theta).
  2. Find dxdx: Differentiate x=2sin⁡(θ)x = 2\sin(\theta) with respect to θ\theta to find dxdx:dxdθ=2cos⁡(θ)\frac{dx}{d\theta} = 2\cos(\theta)dx=2cos⁡(θ)dθdx = 2\cos(\theta)d\theta
  3. Substitute xx and dxdx: Substitute x=2sin⁡(θ)x = 2\sin(\theta) and dx=2cos⁡(θ)dθdx = 2\cos(\theta)d\theta into the integral:\newline∫−716−4(2sin⁡(θ))2⋅2cos⁡(θ)dθ\int\frac{-7}{\sqrt{16-4(2\sin(\theta))^2}} \cdot 2\cos(\theta)d\theta\newlineSimplify the expression under the square root:\newline∫−716−16sin⁡2(θ)⋅2cos⁡(θ)dθ\int\frac{-7}{\sqrt{16-16\sin^2(\theta)}} \cdot 2\cos(\theta)d\theta
  4. Simplify Expression: Recognize that 16sin⁡2(θ)16\sin^2(\theta) is a multiple of the Pythagorean identity, so we can simplify further:\newline∫−716(1−sin⁡2(θ))⋅2cos⁡(θ)dθ\int\frac{-7}{\sqrt{16(1-\sin^2(\theta))}} \cdot 2\cos(\theta)d\theta\newlineSimplify the square root using the identity 1−sin⁡2(θ)=cos⁡2(θ)1 - \sin^2(\theta) = \cos^2(\theta):\newline∫−74cos⁡(θ)⋅2cos⁡(θ)dθ\int\frac{-7}{4\cos(\theta)} \cdot 2\cos(\theta)d\theta
  5. Cancel Cos Terms: Cancel out the cos⁡(θ)\cos(\theta) terms:\newline∫−74cos⁡(θ)⋅2cos⁡(θ)dθ=∫−74⋅2dθ\int\frac{-7}{4\cos(\theta)} \cdot 2\cos(\theta)d\theta = \int\frac{-7}{4} \cdot 2d\theta\newlineSimplify the constant factors:\newline∫−72dθ\int\frac{-7}{2}d\theta
  6. Integrate with Respect: Integrate with respect to theta: (−72)∫dθ=(−72)θ+C(-\frac{7}{2}) \int d\theta = (-\frac{7}{2}) \theta + C
  7. Express Θ\Theta in xx: Now we need to express θ\theta in terms of xx. Since x=2sin⁡(θ)x = 2\sin(\theta), we can write sin⁡(θ)=x2\sin(\theta) = \frac{x}{2}. To find θ\theta, we take the inverse sine (arcsin) of both sides:\newlineθ=arcsin⁡(x2)\theta = \arcsin\left(\frac{x}{2}\right)\newlineSubstitute θ\theta back into the integral result:\newline\(\left(-\frac{\(7\)}{\(2\)}\right) * \theta + C = \left(-\frac{\(7\)}{\(2\)}\right) * \arcsin\left(\frac{x}{\(2\)}\right) + C

More problems from Find indefinite integrals using the substitution

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

View all (263)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant