Full solution
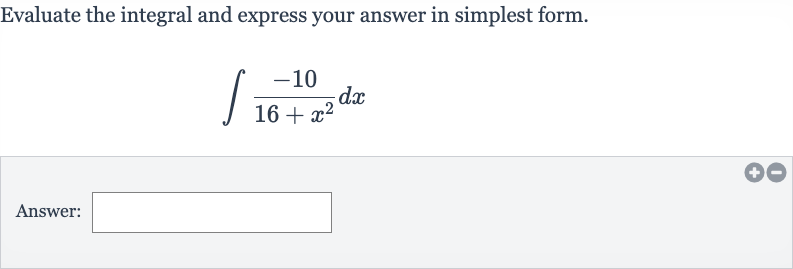
Q. Evaluate the integral and express your answer in simplest form.Answer:
- Recognize Standard Form: We are given the integral: To solve this integral, we can recognize that it is a standard form of the arctangent function, where the integral of is arctan + C, where C is the constant of integration.Let's identify , which gives us .
- Identify Constant: Now we can rewrite the integral by factoring out the constant and substituting :
- Rewrite Integral: Next, we apply the arctangent formula:\(-10 \times \int \frac{}{^+x^{}}dx = \times \left(\frac{}{}\right)\arctan\left(\frac{x}{}\right) + C= \left(-\frac{}{}\right) \times \arctan\left(\frac{x}{}\right) + C= -\frac{}{} \times \arctan\left(\frac{x}{}\right) + C
- Apply Arctangent Formula: We have found the indefinite integral in its simplest form: