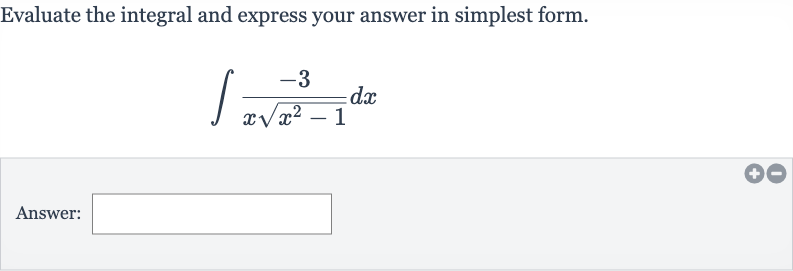
Evaluate the integral and express your answer in simplest form. int(-3)/(xsqrt(x^(2)-1))dx Answer:

Question

Evaluate the integral and express your answer in simplest form.  int(-3)/(xsqrt(x^(2)-1))dx Answer:

Bytelearn · Accepted Answer

Recognize standard form: Recognize the integral as a standard form. The integral ∫(-3)/(x*sqrt(x^2-1))dx can be recognized as a standard form related to the inverse hyperbolic function, specifically the inverse hyperbolic secant function, because the denominator has the form of a hyperbolic identity. We can use the substitution u = x^2 - 1 to simplify the integral.Perform substitution: Perform the substitution. Let u = x^2 - 1, then du = 2xdx. We need to express -3/(x*sqrt(x^2-1))dx in terms of u and du. Since du = 2xdx, we can write dx = du/(2x). Also, since u = x^2 - 1, we have sqrt(x^2 - 1) = sqrt(u).Rewrite in terms of u: Rewrite the integral in terms of u. Substituting the expressions from Step 2 into the integral, we get: ∫(-3)/(x*sqrt(u)) * (du/(2x)) This simplifies to: ∫(-3)/(2*sqrt(u)) duIntegrate with respect to u: Integrate with respect to u. The integral of -3/(2*sqrt(u)) with respect to u is a standard form. We can integrate it directly: ∫(-3)/(2*sqrt(u)) du = -3/2 ∫1/sqrt(u) du The antiderivative of 1/sqrt(u) is 2*sqrt(u), so we have: -3/2 * 2*sqrt(u) + CSimplify the result: Simplify the result. Simplifying the expression from Step 4, we get: -3*sqrt(u) + CBack-substitute u: Back-substitute u with x^2 - 1. Now we need to replace u with our original substitution, u = x^2 - 1, to express the antiderivative in terms of x: -3*sqrt(x^2 - 1) + C

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{-3}{x \sqrt{x^{2}-1}} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral and express your answer in simplest form.\newline∫−3xx2−1dx \int \frac{-3}{x \sqrt{x^{2}-1}} d x ∫xx2−1​−3​dx\newlineAnswer:

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{-3}{x \sqrt{x^{2}-1}} d x$ $\newline$ Answer: