Full solution
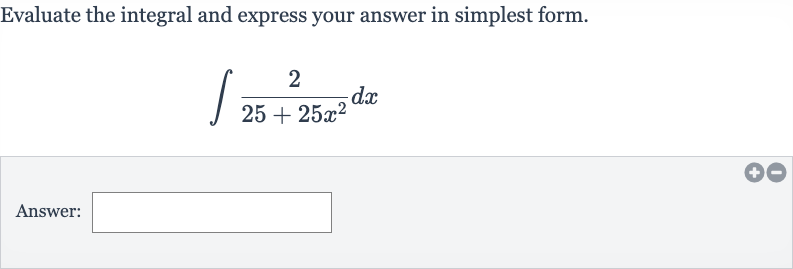
Q. Evaluate the integral and express your answer in simplest form.Answer:
- Factor out common factor: Simplify the integrand by factoring out the common factor of in the denominator. = *
- Recognize standard integral: Recognize that the integral of is a standard integral that corresponds to the arctangent function.
- Multiply by constant factor: Multiply the result of the integral by the constant factor that was factored out in Step .
- Write final answer: Write the final answer, which is the simplest form of the evaluated integral.Answer: