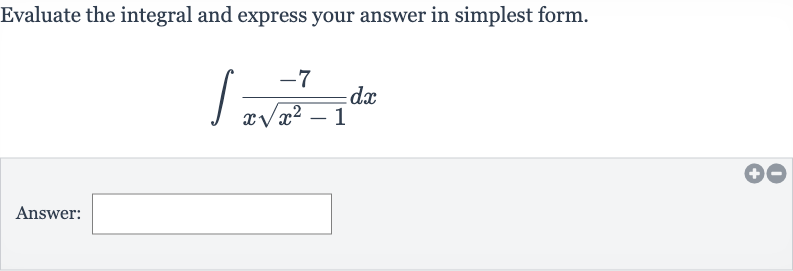
Evaluate the integral and express your answer in simplest form. int(-7)/(xsqrt(x^(2)-1))dx Answer:

Question

Evaluate the integral and express your answer in simplest form.  int(-7)/(xsqrt(x^(2)-1))dx Answer:

Bytelearn · Accepted Answer

Identify Substitution: Let's start by identifying a substitution that can simplify the integral. We notice that the denominator has the expression sqrt(x^2-1), which suggests a trigonometric substitution. Specifically, we can use the substitution x = sec(theta), because then sqrt(x^2-1) would become sqrt(sec^2(theta)-1) = tan(theta). Let's perform this substitution.Find dx in terms of d(theta): First, we need to find dx in terms of d(theta). Since x = sec(theta), we take the derivative of both sides with respect to theta to get dx/d(theta) = sec(theta)tan(theta). Therefore, dx = sec(theta)tan(theta)d(theta).Perform Substitution: Now we substitute x = sec(theta) and dx = sec(theta)tan(theta)d(theta) into the integral. The integral becomes: int(-7)/(sec(theta)*tan(theta)) * sec(theta)tan(theta)d(theta) This simplifies to: int(-7)d(theta)Integrate Constant: The integral of a constant is just the constant times the variable of integration. So we have: -7 * theta + C, where C is the constant of integration.Back-Substitute for x: Now we need to back-substitute to get our answer in terms of x. We originally set x = sec(theta), so we need to solve for theta. We can do this by taking the inverse secant of both sides: theta = arcsec(x).Final Answer: Substituting theta back into our integral result, we get: -7 * arcsec(x) + C This is our final answer in terms of x.

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{-7}{x \sqrt{x^{2}-1}} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Evaluate the integral and express your answer in simplest form.\newline∫−7xx2−1dx \int \frac{-7}{x \sqrt{x^{2}-1}} d x ∫xx2−1​−7​dx\newlineAnswer:

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{-7}{x \sqrt{x^{2}-1}} d x$ $\newline$ Answer: