Full solution
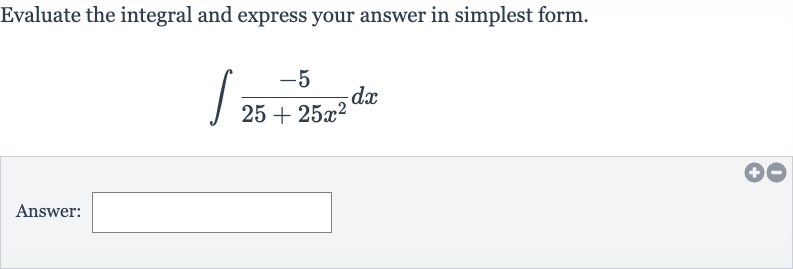
Q. Evaluate the integral and express your answer in simplest form.Answer:
- Factor out constant: Simplify the integral by factoring out the constant from the denominator.
- Recognize arctangent form: Recognize that the integral is now in the form of the arctangent function derivative.
- Evaluate using arctangent: Evaluate the integral using the arctangent function.
- Write final answer: Write the final answer.Answer: