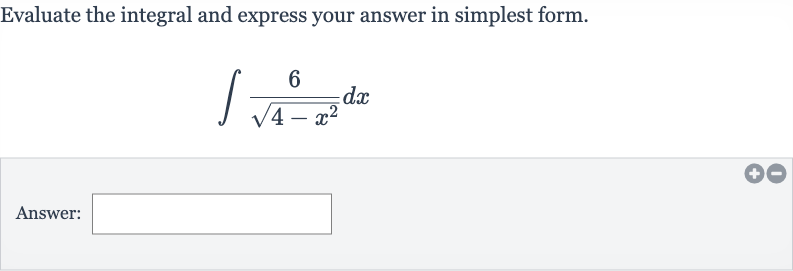
Evaluate the integral and express your answer in simplest form. int(6)/(sqrt(4-x^(2)))dx Answer:

Question

Evaluate the integral and express your answer in simplest form.  int(6)/(sqrt(4-x^(2)))dx Answer:

Bytelearn · Accepted Answer

Recognize standard form: Recognize the integral as a standard form. The integral ∫6/(sqrt(4-x^2))dx resembles the integral of the form ∫du/sqrt(a^2-u^2), which is a standard inverse trigonometric integral.Trigonometric substitution: Use a trigonometric substitution. Let x = 2sin(θ), which implies dx = 2cos(θ)dθ. The limits of integration will change accordingly if this were a definite integral, but since it's an indefinite integral, we will substitute back to x at the end.Substitute x with 2sin(θ): Substitute x with 2sin(θ) in the integral. The integral becomes ∫6/(sqrt(4-(2sin(θ))^2)) * 2cos(θ)dθ.Simplify the integral: Simplify the integral. The integral simplifies to ∫6/(sqrt(4-4sin^2(θ))) * 2cos(θ)dθ = ∫6/(sqrt(4(1-sin^2(θ)))) * 2cos(θ)dθ.Use Pythagorean identity: Use the Pythagorean identity sin^2(θ) + cos^2(θ) = 1. The integral further simplifies to ∫6/(2sqrt(cos^2(θ))) * 2cos(θ)dθ = ∫6/cos(θ) * 2cos(θ)dθ.Cancel cos(θ) terms: Cancel out the cos(θ) terms. The integral simplifies to ∫6 * 2dθ = ∫12dθ.Integrate with respect to θ: Integrate with respect to θ. The integral of 12 with respect to θ is 12θ.Substitute back to x: Substitute back to x using the original substitution x = 2sin(θ). We need to solve for θ in terms of x. Since x = 2sin(θ), we have sin(θ) = x/2. Therefore, θ = arcsin(x/2).Write final answer: Write the final answer. The final answer is 12θ + C, where C is the constant of integration. Substituting θ back, we get 12arcsin(x/2) + C.

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{6}{\sqrt{4-x^{2}}} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral and express your answer in simplest form.\newline∫64−x2dx \int \frac{6}{\sqrt{4-x^{2}}} d x ∫4−x2​6​dx\newlineAnswer:

Evaluate the integral and express your answer in simplest form. $\newline$ $\int \frac{6}{\sqrt{4-x^{2}}} d x$ $\newline$ Answer: