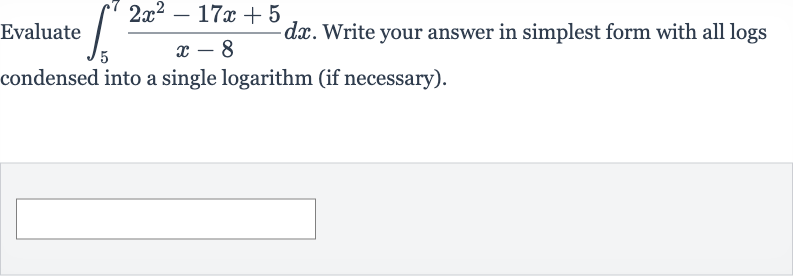
Evaluate int_(5)^(7)(2x^(2)-17 x+5)/(x-8)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Question

Evaluate  int_(5)^(7)(2x^(2)-17 x+5)/(x-8)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Bytelearn · Accepted Answer

Perform Polynomial Long Division: Perform polynomial long division to simplify the integrand. We need to divide the polynomial 2x^2 - 17x + 5 by x - 8. 2x^2 - 17x + 5 : (x - 8) = 2x + 1 with a remainder of 21x - 3. So, (2x^2 - 17x + 5)/(x - 8) = 2x + 1 + (21x - 3)/(x - 8).Write Integral with Simplified Integrand: Write the integral with the simplified integrand. Now we can write the integral as: ∫ from 5 to 7 of (2x + 1 + (21x - 3)/(x - 8)) dx. This can be split into three separate integrals: ∫ from 5 to 7 of 2x dx + ∫ from 5 to 7 of 1 dx + ∫ from 5 to 7 of (21x - 3)/(x - 8) dx.Integrate Each Term Separately: Integrate each term separately. The first integral is ∫ from 5 to 7 of 2x dx = x^2 evaluated from 5 to 7. The second integral is ∫ from 5 to 7 of 1 dx = x evaluated from 5 to 7. For the third integral, we need to split the fraction into two parts: ∫ from 5 to 7 of 21x/(x - 8) dx - ∫ from 5 to 7 of 3/(x - 8) dx.Simplify Third Integral Further: Simplify the third integral further. The term 21x/(x - 8) can be rewritten as 21 + 168/(x - 8) by polynomial long division. So, ∫ from 5 to 7 of 21x/(x - 8) dx = ∫ from 5 to 7 of 21 dx + ∫ from 5 to 7 of 168/(x - 8) dx. Now we have four integrals to evaluate: ∫ from 5 to 7 of 2x dx, ∫ from 5 to 7 of 1 dx, ∫ from 5 to 7 of 21 dx, and ∫ from 5 to 7 of (168/(x - 8) - 3/(x - 8)) dx.Evaluate Definite Integrals: Evaluate the definite integrals. The first integral: ∫ from 5 to 7 of 2x dx = x^2 evaluated from 5 to 7 = 7^2 - 5^2 = 49 - 25 = 24. The second integral: ∫ from 5 to 7 of 1 dx = x evaluated from 5 to 7 = 7 - 5 = 2. The third integral: ∫ from 5 to 7 of 21 dx = 21x evaluated from 5 to 7 = 21*7 - 21*5 = 147 - 105 = 42. The fourth integral: ∫ from 5 to 7 of (168/(x - 8) - 3/(x - 8)) dx = ∫ from 5 to 7 of 165/(x - 8) dx.Evaluate Fourth Integral: Evaluate the fourth integral. The fourth integral is ∫ from 5 to 7 of 165/(x - 8) dx = 165 * ln|x - 8| evaluated from 5 to 7. This gives us 165 * ln|7 - 8| - 165 * ln|5 - 8| = 165 * ln|-1| - 165 * ln|-3|. Since the natural logarithm of a negative number is not defined in the real number system, we have made a mistake. We should have used the absolute value inside the logarithm.

Evaluate $\int_{5}^{7} \frac{2 x^{2}-17 x+5}{x-8} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Evaluate ∫572x2−17x+5x−8dx \int_{5}^{7} \frac{2 x^{2}-17 x+5}{x-8} d x ∫57​x−82x2−17x+5​dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Evaluate $\int_{5}^{7} \frac{2 x^{2}-17 x+5}{x-8} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).