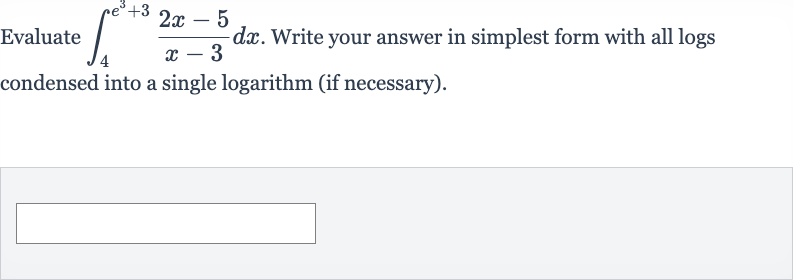
Evaluate int_(4)^(e^(3)+3)(2x-5)/(x-3)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Question

Evaluate  int_(4)^(e^(3)+3)(2x-5)/(x-3)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Bytelearn · Accepted Answer

Perform Long Division: We have the integral: int_(4)^(e^(3)+3)(2x-5)/(x-3)dx First, we will perform long division on the integrand to simplify the expression. (2x-5)/(x-3) can be divided to get 2 with a remainder of -1: 2x-5 = 2(x-3) - 1 So, (2x-5)/(x-3) = 2 - 1/(x-3) Now, we can rewrite the integral as: int_(4)^(e^(3)+3)(2 - 1/(x-3))dxSeparate into Simpler Integrals: Next, we separate the integral into two simpler integrals: int_(4)^(e^(3)+3)2dx - int_(4)^(e^(3)+3)1/(x-3)dx Now we can integrate each term separately. The integral of a constant is just the constant times the variable, and the integral of 1/(x-3) is the natural logarithm of the absolute value of (x-3). So we have: 2x - ln|x-3| evaluated from 4 to e^(3)+3.Evaluate Antiderivative at Limits: Now we evaluate the antiderivative at the upper and lower limits of integration: (2(e^(3)+3) - ln|e^(3)+3-3|) - (2(4) - ln|4-3|) Simplify the expressions: (2e^(3)+6 - ln|e^(3)|) - (8 - ln|1|) Since ln|e^(3)| = 3 (because e^(3) is positive, we don't need the absolute value) and ln|1| = 0, we get: (2e^(3)+6 - 3) - (8 - 0)Perform Subtraction: Now we perform the subtraction: 2e^(3)+6 - 3 - 8 = 2e^(3) - 5 This is the value of the definite integral.

Evaluate $\int_{4}^{e^{3}+3} \frac{2 x-5}{x-3} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Evaluate ∫4e3+32x−5x−3dx \int_{4}^{e^{3}+3} \frac{2 x-5}{x-3} d x ∫4e3+3​x−32x−5​dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Evaluate $\int_{4}^{e^{3}+3} \frac{2 x-5}{x-3} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).