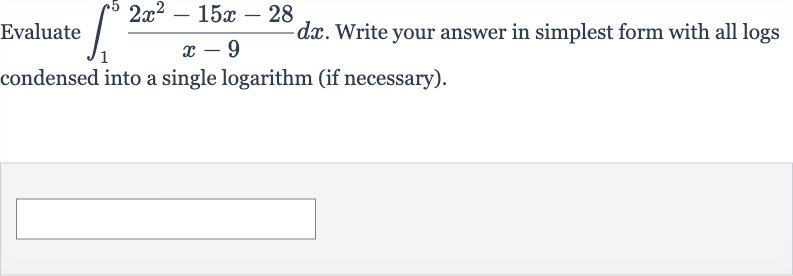
Evaluate int_(1)^(5)(2x^(2)-15 x-28)/(x-9)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Question

Evaluate  int_(1)^(5)(2x^(2)-15 x-28)/(x-9)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Bytelearn · Accepted Answer

Perform Polynomial Long Division: Perform polynomial long division to simplify the integrand. We need to divide the polynomial 2x^2 - 15x - 28 by x - 9.Long Division Calculation: Polynomial long division calculation. 2x^2 - 15x - 28 : (x - 9) = 2x + 3 with a remainder of 1. So, (2x^2 - 15x - 28)/(x - 9) = 2x + 3 + 1/(x - 9).Set Up Integral: Set up the integral with the simplified integrand. int_(1)^(5)(2x + 3 + 1/(x - 9))dx = int_(1)^(5)2xdx + int_(1)^(5)3dx + int_(1)^(5)1/(x - 9)dx.Evaluate Integrals: Evaluate the integrals separately. First, int_(1)^(5)2xdx = [x^2]_(1)^(5) = 5^2 - 1^2 = 25 - 1 = 24. Second, int_(1)^(5)3dx = [3x]_(1)^(5) = 3*5 - 3*1 = 15 - 3 = 12. Third, int_(1)^(5)1/(x - 9)dx = [ln|x - 9|]_(1)^(5) = ln|5 - 9| - ln|1 - 9| = ln|4| - ln|8|.Combine Integral Results: Combine the results of the integrals. The integral from 1 to 5 of (2x^2 - 15x - 28)/(x - 9)dx is 24 + 12 + ln|4| - ln|8|.Condense Logarithms: Condense the logarithms into a single logarithm. ln|4| - ln|8| = ln(|4|/|8|) = ln(1/2).Final Answer: Combine all terms to get the final answer. The final answer is 24 + 12 + ln(1/2) = 36 + ln(1/2).

Evaluate $\int_{1}^{5} \frac{2 x^{2}-15 x-28}{x-9} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Evaluate ∫152x2−15x−28x−9dx \int_{1}^{5} \frac{2 x^{2}-15 x-28}{x-9} d x ∫15​x−92x2−15x−28​dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Evaluate $\int_{1}^{5} \frac{2 x^{2}-15 x-28}{x-9} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).