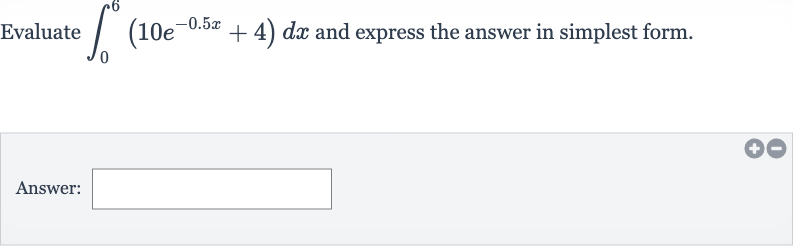
Evaluate int_(0)^(6)(10e^(-0.5 x)+4)dx and express the answer in simplest form. Answer:

Question

Evaluate  int_(0)^(6)(10e^(-0.5 x)+4)dx and express the answer in simplest form. Answer:

Bytelearn · Accepted Answer

Integrate first part: Now we will integrate the first part, ∫10e^(-0.5x)dx. The integral of e^(ax) with respect to x is (1/a)e^(ax), so the integral of 10e^(-0.5x) is: ∫10e^(-0.5x)dx = -20e^(-0.5x)Integrate second part: Next, we integrate the second part, ∫4dx. The integral of a constant is just the constant times the variable, so: ∫4dx = 4xCombine integrals: Now we combine the two integrals to get the indefinite integral: ∫(10e^(-0.5x) + 4)dx = -20e^(-0.5x) + 4x + C Since we are evaluating a definite integral from 0 to 6, we do not need to include the constant of integration C.Evaluate at upper limit: We evaluate the indefinite integral at the upper limit of integration, x = 6: -20e^(-0.5*6) + 4*6 = -20e^(-3) + 24Evaluate at lower limit: Next, we evaluate the indefinite integral at the lower limit of integration, x = 0: -20e^(-0.5*0) + 4*0 = -20e^(0) + 0 = -20Find definite integral: We subtract the value of the indefinite integral at the lower limit from the value at the upper limit to find the definite integral: (-20e^(-3) + 24) - (-20) = -20e^(-3) + 24 + 20Simplify final answer: Now we simplify the expression to find the final answer: -20e^(-3) + 24 + 20 = -20/e^3 + 44

Evaluate $\int_{0}^{6}\left(10 e^{-0.5 x}+4\right) d x$ and express the answer in simplest form. $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate ∫06(10e−0.5x+4)dx \int_{0}^{6}\left(10 e^{-0.5 x}+4\right) d x ∫06​(10e−0.5x+4)dx and express the answer in simplest form.\newlineAnswer:

Evaluate $\int_{0}^{6}\left(10 e^{-0.5 x}+4\right) d x$ and express the answer in simplest form. $\newline$ Answer: