Full solution
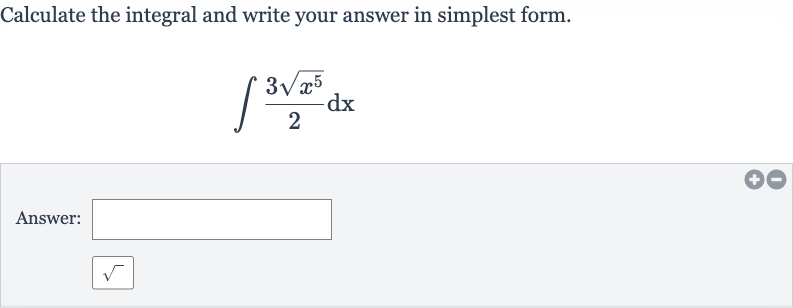
Q. Calculate the integral and write your answer in simplest form.Answer:
- Rewrite integral: Rewrite the integral in a more convenient form for integration.The integral of can be rewritten by expressing the square root as a power of .
- Apply power rule: Apply the power rule for integration.The power rule states that , where is the constant of integration.
- Simplify expression: Simplify the expression.Now we simplify the exponent and the fraction.
- Final answer: Write the final answer in simplest form.The integral in simplest form is: