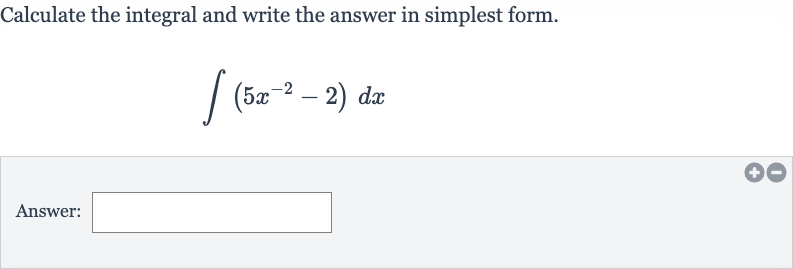
Calculate the integral and write the answer in simplest form. int(5x^(-2)-2)dx Answer:

Question

Calculate the integral and write the answer in simplest form.  int(5x^(-2)-2)dx Answer:

Bytelearn · Accepted Answer

Identify Integral: Identify the integral to be solved. We need to find the indefinite integral of the function 5x^(-2)-2 with respect to x. The integral is written as ∫(5x^(-2)-2)dx.Break Down: Break down the integral into simpler parts. The integral of a sum is the sum of the integrals, so we can write: ∫(5x^(-2)-2)dx = ∫5x^(-2)dx - ∫2dx.Integrate Separately: Integrate each term separately. For the first term, ∫5x^(-2)dx, we use the power rule of integration, which states that ∫x^n dx = x^(n+1)/(n+1) + C, where n ≠ -1. Applying the power rule, we get: ∫5x^(-2)dx = 5 * ∫x^(-2)dx = 5 * (-x^(-1)) + C1 = -5/x + C1, where C1 is a constant of integration.Integrate Second Term: Integrate the second term. For the second term, ∫2dx, the integral of a constant is the constant times the variable of integration plus another constant of integration. So, ∫2dx = 2x + C2, where C2 is another constant of integration.Combine Results: Combine the results of the two integrals. Combining the results from Step 3 and Step 4, we get: ∫(5x^(-2)-2)dx = -5/x + 2x + C1 + C2. Since C1 and C2 are arbitrary constants, we can combine them into a single constant, C. Therefore, the integral is: ∫(5x^(-2)-2)dx = -5/x + 2x + C.

Calculate the integral and write the answer in simplest form. $\newline$ $\int\left(5 x^{-2}-2\right) d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Calculate the integral and write the answer in simplest form.\newline∫(5x−2−2)dx \int\left(5 x^{-2}-2\right) d x ∫(5x−2−2)dx\newlineAnswer:

Calculate the integral and write the answer in simplest form. $\newline$ $\int\left(5 x^{-2}-2\right) d x$ $\newline$ Answer: